定義
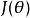 費希爾信息
費希爾信息品質函式的方差稱為費希爾信息,用表示,定義為:
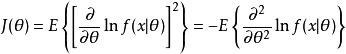 費希爾信息
費希爾信息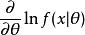 費希爾信息
費希爾信息其中,為品質函式,其均值為零。
介紹
Fisher信息是一種測量可觀察隨機變數X攜帶的關於X的機率所依賴的未知參數θ的信息量的方式。 令f(X;θ)為X的機率密度函式(或機率質量函式),條件是θ的值。 這也是θ的似然函式。 它描述了在給定已知的θ值的情況下觀察給定樣本X的機率。 如果f相對於θ的變化急劇地達到峰值,則很容易從數據中指示θ的“正確”值,或者等效地,數據X提供關於參數θ的大量信息。 如果似然f是平坦的並且展開,則需要許多很多樣本(如X)來估計使用整個採樣群體獲得的θ的實際“真實”值。 這表明研究了關於θ的某種方差。
套用
實驗的最佳化設計
Fisher信息廣泛用於最佳實驗設計。由於估計器 - 方差和Fisher信息的互易性,最小化方差對應於最大化信息。
當線性(或線性化)統計模型具有多個參數時,參數估計器的均值是向量,其方差是矩陣。方差矩陣的逆被稱為“信息矩陣”。因為參數矢量的估計量的方差是矩陣,所以“最小化方差”的問題是複雜的。統計學家使用統計理論,使用實值匯總統計數據壓縮信息矩陣;作為實值函式,這些“信息標準”可以最大化。
傳統上,統計學家通過考慮協方差矩陣(無偏估計量)的一些匯總統計量來評估估計量和設計,通常具有正實數值(如行列式或矩陣跡線)。使用正實數帶來了幾個優點:如果單個參數的估計具有正方差,則方差和Fisher信息都是正實數;因此它們是非負實數的凸錐的成員(其非零成員在同一個錐體中具有倒數)。對於幾個參數,協方差矩陣和信息矩陣是在Loewner(Löwner)階下在部分有序向量空間中非負定對稱矩陣的凸錐的元素。該錐體在矩陣加法和反演下以及在正實數和矩陣的乘法下閉合。 Pukelsheim出現了矩陣理論和Loewner秩序的論述。
傳統的最優性標準是信息矩陣的不變數,在不變數理論意義上;在代數上,傳統的最優性標準是(Fisher)信息矩陣的特徵值的函式(參見最優設計 )。
傑弗里斯先前在貝葉斯統計中
在貝葉斯統計中,Fisher信息用於計算Jeffreys先驗,這是連續分布參數的標準無信息先驗。
計算神經科學
Fisher信息已被用於發現神經代碼準確性的界限。在那種情況下,X通常是表示低維變數θ(例如刺激參數)的許多神經元的聯合回響。特別是研究了相關性在神經反應噪聲中的作用。
物理定律的推導
費舍爾信息在弗里登提出的有爭議的原則中起著核心作用,該原則是物理定律的基礎,這一主張一直存在爭議。
機器學習
Fisher信息用於機器學習技術,如彈性權重合併,它可以減少人工神經網路中的災難性遺忘。
