SWAR算法“計算漢明重量”
第一步:
計算出來的值i的二進制可以按每2個二進制位為一組進行分組,各組的十進制表示的就是該組的漢明重量。
第二步:
計算出來的值i的二進制可以按每4個二進制位為一組進行分組,各組的十進制表示的就是該組的漢明重量。
第三步:
計算出來的值i的二進制可以按每8個二進制位為一組進行分組,各組的十進制表示的就是該組的漢明重量。
第四步:
i * (0x01010101)計算出漢明重量並記錄在二進制的高八位,>>24語句則通過右移運算,將漢明重量移到最低八位,最後二進制對應的十進制數就是漢明重量。
算法時間複雜度是O(1)的。
相關代碼
實現
 圖一
圖一在密碼學以及其它套用中經常需要計算數據位中1的個數,針對如何高效地實現人們已經廣泛地進行了研究。一些處理器使用單個的命令進行計算,另外一些根據數據位向量使用並行運算進行處理。對於沒有這些特性的處理器來說,已知的最好解決辦法是按照樹狀進行相加。例如,要計算二進制數A=0110110010111010中1的個數,這些運算可以表示為圖一:
這裡的運算是用C語言表示的,所以X >> Y表示X右移Y位,X & Y表示X與Y的位與,+表示普通的加法。基於上面所討論的思想的這個問題的最好算法列在這裡:
在最壞的情況下,上面的實現是所有已知算法中表現最好的。但是,如果已知大多數數據位是0的話,那么還有更快的算法。這些更快的算法是基於這樣一種事實即X與X-1相 與得到的最低位永遠是0。例如圖二:
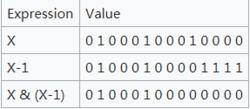 圖二
圖二減1操作將最右邊的符號從0變到1,從1變到0, 與操作將會移除最右端的1。如果最初X有N個1,那么經過N次這樣的疊代運算,X將減到0。下面的算法就是根據這個原理實現的。

