理想加白噪聲情況下香農限
考慮數據率、噪聲以及誤碼率的關係。噪聲的存在會破壞一個或多個比特。假如數據率增加,那么這些比特會變短,因而給定的噪聲模式會影響更多個比特。於是,給定一個噪聲值,數據率越高則誤碼率也越高。所有的這些概念可以通過香農公式清楚聯繫在一起,此公式由數學家 克勞德·艾爾伍德·香農(Claude Elwood Shannon,1916-2001)推導得出的。
如剛才所描繪的,數據率越高,無用的噪聲會帶來更嚴重的破壞。在噪聲存在的情況下,給點一個噪聲值,我們能夠通過提高信號強度來提高正確接收數據的能力。在這一推導過程中涉及的主要參數是信噪比(SNR或S/N),它是指在傳輸過程中某一點的信號功率與噪聲包含功率之比。通常信噪比在接收器處測量,因為正是在這裡我們試圖處理信號並消除無用噪聲。為了使用方便,這個比率通常用分貝表示
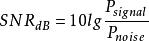 香農限
香農限它表示有用信號超出噪聲值的量,以分貝為單位。SNR的值越高,表示信號的質量越好,所需中間轉發器的數量越少。
信噪比對數字數據傳輸十分重要,因為它限定了一個可達到的數據率上限。香農得出的結果是,用bps來表示的信道的最大容量遵從等式
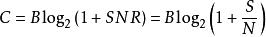 香農限
香農限C是以比特/秒為單位的信道容量,淨比特率的理論上限(信息速率,有時表示為I),不包括糾錯碼;
B是頻寬的信道的在赫茲(通帶中的帶通信號的情況下的頻寬);
S是以瓦(或伏平方)測量的頻寬上的平均接收信號功率(在載波調製通帶傳輸的情況下,通常表示為C);
N是噪聲和頻寬上的干擾的平均功率,以瓦(或伏特平方)為單位測量;
S / N是通信信號對接收機噪聲和干擾的信噪比(SNR)或載波噪聲比(CNR)(表示為線性功率比,而不是對數分貝) 。
香農公式顯示出理論上可達到的最大值。然而在實際套用中能夠達到的速率要低得多。其中一個原因是該公式假定噪聲為白噪聲(熱噪聲),既沒有考慮到衝激噪聲,也沒有考慮衰減和時延失真。即使在理想白噪聲情況下,因為編碼的原因(如編碼長度和複雜性等),目前的技術仍然無法達到香農容量。
香農公式中提到的容量為無誤碼容量。經香農證明,假如信道上的實際信息率比無誤碼容量低,從理論上來說,通過適當的信息編碼,信道就有可能達到無誤碼容量。遺憾的是,香農的理論並沒有給出如何找到這種編碼的方法,但提供了一個用來衡量實際通信機制性能的計算標準。
通過香農公式我們可以考慮如何將信道容量上限提高。假如噪聲值給定,那么似乎通過增加信號強度或頻寬就能提高數據率;但是,如果信號強度增加了,則系統的非線性程度也會提高,這就導致互調噪聲的增加。還有一點需要注意,由於假定噪聲是白噪聲,那么頻寬越寬,因此系統容納的噪聲也就越多,因此隨著B的增加SNR反而降低了。
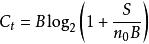 香農限
香農限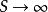 香農限
香農限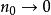 香農限
香農限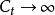 香農限
香農限當 ,或 時, 。
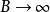 香農限
香農限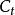 香農限
香農限但是當 時, 將趨向何值?
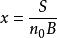 香農限
香農限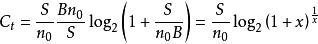 香農限
香農限令
,上式可以改寫為: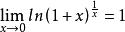 香農限
香農限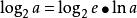 香農限
香農限利用關係式:
上式變為:
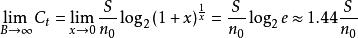 香農限
香農限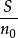 香農限
香農限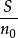 香農限
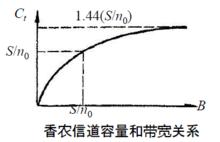
香農限上式表明,當給定 時,若頻寬B趨於無窮大,信道容量不會趨於無限大,而只是 的1.44倍。這是
因為當頻寬B增大時,噪聲功率也隨之增大。
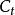 香農限
香農限和頻寬B的關係曲線:
 香農限
香農限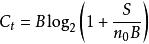 香農限
香農限上式還可以改寫成如下形式:
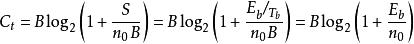 香農限
香農限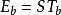 香農限
香農限式中 ——每比特能量
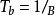 香農限
香農限——每比特持續時間
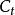 香農限
香農限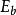 香農限
香農限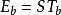 香農限
香農限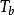 香農限
香農限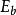 香農限
香農限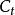 香農限
香農限上式表明,為了得到給定的信道容量 ,可以增大頻寬B以換取 的減小;另一方面,在接收功率受 限的情況下,由於 ,可以增大 以減小S來保持 和 不變。
香農定理與香農限
香農定理概述
在信息理論中,噪聲信道編碼定理(有時是香農定理)確定了對於通信信道的任何給定程度的噪聲污染,可以將幾乎無錯誤的離散數據(數字信息)傳送到可計算的最大值通過渠道率。這個結果由克勞德·香農在1948年提出,部分原因是早期的工作和哈里·奈奎斯特(Harry Nyquist)和拉爾夫·哈特利(Ralph Hartley)的觀點。
香農定理指出,給定具有信道容量C和以速率R傳送的信息的噪聲信道,則if R <C 存在碼,其允許誤差的機率,以做得任意小,在接收器處。這意味著理論上可以以低於限制速率C的速度將信息幾乎無差錯地傳送出去。
相反也是重要的。如果 R> C,任意小的錯誤機率是無法實現的。所有代碼將具有大於某個正極小水平的誤差機率,並且該水平隨著速率的增加而增加。因此,不能保證通過信道容量以外的速率可靠地傳輸信息。定理沒有解決速度和能力相等的罕見情況。
信道容量C可以根據信道的物理性質來計算;
數學概述
 香農限
香農限對於每個離散的無記憶通道,通道容量
1.對於每個離散的無記憶通道,通道容量
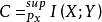 香農限
香農限具有以下屬性。對於任何ε> 0且- [R <C,對於足夠大Ñ,存在的長度的代碼Ñ和速率≥[R和解碼算法, 使得塊差錯的最大機率≤ε。
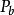 香農限
香農限2.如果位錯誤 的機率是可以接受的,則可以實現高達 R()的速率,其中
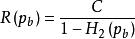 香農限
香農限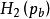 香農限
香農限和 是二進制熵函式
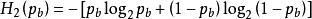 香農限
香農限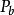 香農限
香農限(MacKay(2003),第162頁; cf Gallager(1968),ch.5; Cover和Thomas(1991),第198頁; Shannon(1948)11頁)
香農哈特利定律
概述
在資訊理論中,香農極限告訴在該信息可以通過一個特定頻寬的存在特定噪聲的通信信道數據被傳送的最大速率。這是噪聲信道編碼定理在受到高斯噪聲的連續時間、模擬通信信道的原型情況下的套用。該定理建立了對這種通信鏈路的信道香農限,限制了在存在噪聲干擾的情況下可以以指定頻寬傳送的每個時間單位的無錯誤信息的最大量,假設信號功率是有界的,並且高斯噪聲過程的特徵在於已知功率或功率譜密度。定理以Claude Shannon和Ralph Hartley命名。
香農 - 哈特利定理陳述了通道容量C,這意味著可以使用平均接收信號功率S通過經過加性白高斯的模擬通信通道以任意低的錯誤率傳送的數據的信息速率的理論上的最上限電源噪聲N:
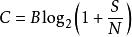 香農限
香農限奈奎斯特率
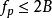 香農限
香農限在1927年,奈奎斯特認為每單位時間可以通過電報通道的獨立脈衝數量被限制在通道頻寬的兩倍。在符號中,
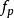 香農限
香農限其中 是脈衝頻率(以每秒脈衝數計), B是頻寬(赫茲)。數量2 B後來被稱為奈奎斯特速率,並以每秒2個 B脈衝的限制脈衝速率以奈奎斯特率傳送信號。奈奎斯特在1928年發表他的研究成果,作為他的論文“電訊傳播理論中的某些話題”的一部分。
哈特利定律
1928年,哈特利制定了一種量化信息和線路速率(也稱為數據信令速率 R比特每秒)的方法。這種方法,後來被稱為哈特利定律,成為香農更加複雜的通道容量概念的重要前身。
哈特利認為,可以通過通信信道可靠地傳送和接收的可區分脈衝電平的最大數量受到信號幅度的動態範圍和接收機能夠區分振幅電平的精度的限制。具體地說,如果傳送信號的幅度被限制在[ - A ... + A ]伏的範圍內,並且接收機的精度為± ΔV伏特,則不同脈衝M的最大數量由
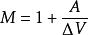 香農限
香農限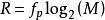 香農限
香農限通過以比特/脈衝中的每個脈衝獲取信息作為可以傳送的不同訊息M的數量的基2-對數,Hartley構建了線速率R的度量: ,
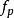 香農限
香農限其中 是脈衝速率,也稱為符號速率,以符號/秒或波特率表示。
然後,哈特利將上述量化與奈奎斯特的觀察結合起來,可以通過頻寬B 赫茲通道的獨立脈衝數為每秒2B脈衝,以達到其可實現線速率的定量測量。
哈特利定律有時引述只是模擬頻寬,B,以Hz為單位,和今天被稱為數字頻寬的R ,以比特/秒為單位之間的比例。其他時候,以這種更定量的形式引用,作為每秒可用的R比特率:
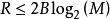 香農限
香農限哈特利沒有確切地知道數字M應如何依賴於信道的噪聲統計,或者即使單個符號脈衝不能可靠地區分為M個等級,通信如何可靠地生成; 利用高斯噪聲統計,系統設計人員必須選擇非常保守的M值來實現低錯誤率。
哈特利的速率結果可以被看作是一個無差錯的能力中號的2個進制信道B每秒符號。有些作者將其稱為容量。但是這樣一個無誤的信道是一個理想化的方式,如果選擇M小到足以使噪聲信道幾乎無誤,結果必然小於頻寬B的噪聲信道的香農容量,這是隨後的香農哈特利定律結果後來。
哈特利定律與香農限的關係
將信道容量與哈特利定律的信息比率進行比較,我們可以找到有效數量的可區分級別M:
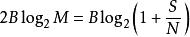 香農限
香農限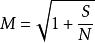 香農限
香農限平方根有效地將功率比轉換回電壓比,因此電平數量幾乎與信號RMS幅度與噪聲標準偏差之比成正比。 香農限與哈特利定律之間形式的相似性不應該被解釋為意味著M脈衝水平可以毫無混亂地被傳送; 需要更多的級別,以允許冗餘編碼和糾錯,但是可以用編碼處理的淨數據速率等同於使用哈特利定律中的M。
可替代形式
頻率依賴(彩色噪聲)情況
在上面的簡單版本中,信號和噪聲完全不相關,在這種情況下,S + N是接收信號和噪聲的總功率。通過對多個窄獨立的高斯信道並行處理信道,獲得加性噪聲不是白色(或S / N在頻寬上的頻率不恆定)的情況下的上述等式的推廣,
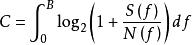 香農限
香農限C是以比特/秒為單位的信道容量 ;
B是信道的頻寬,單位為Hz;
S(f)是信號功率譜
N(f)是噪聲功率譜
f是以Hz為單位的頻率。
注意:該定理僅適用於高斯穩定過程噪聲。該公式引入頻率相關噪聲的方法不能描述所有的連續時間噪聲過程。例如,考慮噪聲過程,其包括在任何時間點加上振幅為1或-1的隨機波,以及將這樣的波加到源信號上的信道。這樣的波的頻率分量是高度依賴的。雖然這樣的噪聲可能具有高功率,但是如果底層噪聲是每個頻帶中的獨立噪聲之和,則傳輸比所需要的功率少得多的連續信號是相當容易的。
近似
對於大或小且恆定的信噪比,容量公式(香農公式)可以近似為:
如果S / N >> 1,那么
1.如果S / N >> 1,那么
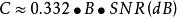 香農限
香農限這裡
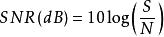 香農限
香農限2. 同理,如果S / N <<1,那么
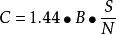 香農限
香農限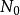 香農限
香農限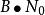 香農限
香農限在這種低SNR近似中,如果噪聲為白色,則光譜密度的容量與頻寬無關
瓦特/赫茲,在這種情況下,總 噪聲功率是。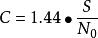 香農限
香農限非靜止記憶信道的信道容量
我們假設通道是無記憶的,但是其轉換機率隨時間而變化,以發射機和接收機已知的方式。
然後通道容量由
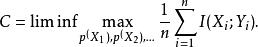 香農限
香農限在每個相應通道的容量達到分配的情況下達到最大值。也就是,
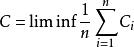 香農限
香農限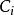 香農限
香農限這裡 代表第i個信道的容量。
各種編碼對於接近香農限的程度
諸如“傳送訊息3次並且如果副本不同則使用最佳2投票方案”這樣的簡單方案是無效率的糾錯方法,不能夠漸近地保證一個數據塊可以毫無差錯地傳達。諸如Reed-Solomon碼的高級技術,以及最近的低密度奇偶校驗(LDPC)碼和turbo碼更接近於達到理論香農限制,但是以高的計算複雜度為代價。使用這些高效率的代碼和當今數位訊號處理器的計算能力,現在可以達到非常接近香農限額。實際上,已經表明,LDPC碼可以達到香農極限的0.0045dB(對於二進制AWGN信道,具有非常長的塊長度)。
土耳其畢爾肯大學教授Erdal Arikan於2009年正式提出的新型編碼方案——極化碼(polar code) ,是目前唯一一個在理論上已經被證明可以到達香農限的方案。

