基本介紹
滑繩線分析滑繩線是在物理中常見的一種曲線，繩子一端結牢在天花板上一點O，另一端穿過固定在天花板上的定滑輪M以後，在下端掛一個重物K，在O與M之間的一段繩子上套了一個小環，可以沿繩子滑動，環下面掛了另一重物G，設重物K在某高度時，小環滑到一點A處使整個系統平衡，當K改變高度時，平衡點A的軌跡稱為滑繩線，如圖，用向量g，k分別表示重物G，K的拉力，s表示繩子最左部分的拉力，根據力的合成法則得：
滑繩線
滑繩線消去|s|得|g|cos α=|k|(sin βcos α+cos β sin α)，設|OM|=l，|k|/|g|=a/l，A(x，y)，將
滑繩線
滑繩線代入化簡得滑繩線的方程
滑繩線當l=a時就是環索線 。
問題分析
考慮一個物理問題，如圖1，有一根繩子，一端結牢在天花板上的一點O，另一端穿過固定在天花板上的定滑輪M以後，在下端掛一個重物K，在O與M之間的一段繩子上套了一個小環，可以沿繩子滑動，環下面掛了另一重物G，設重物K在某高度時，小環滑到一點且處使整個系統平衡，求當K改變高度時，平衡點A的軌跡 。
 圖1 |  圖2 |
滑繩線
滑繩線
滑繩線 滑繩線 滑繩線 滑繩線為了解答這個問題，我們注意，在平衡點A處，究竟受到哪些力的作用?首先由於懸掛重物G，使環A受到一個豎直向下的力，記成。其次由於繩子穿過滑輪M後懸掛重物K，使得點A受到一個沿著AM方向的力，記成，這兩個力的合力把OA這段繩子拉直，並在A點處與AO這段繩子的張力達到平衡，可見合力是沿著射線OA的方向(圖2)，設在運動的某一瞬間，繩子的OA部分與水平面的夾角為α，AM與水平面的夾角為β，由於力是力和力的合力，根據力的合成法則，從圖2中的平行四邊形得到
滑繩線
滑繩線
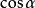滑繩線
滑繩線將其中第一式乘以 ，第二式乘以然後相加，整理得
滑繩線現在設線段OM的長度為l，選取直角坐標系，使O為原點，OM為x軸正方向，y軸的正方向豎直向上，設A的坐標為(x，y)，則從圖2得
滑繩線
滑繩線把它們代入（1）式得到
滑繩線記
滑繩線上式可化為
滑繩線化簡後得到
滑繩線這就是所求軌跡的方程，這個方程所表示的曲線叫做滑繩線。本問題中小環A的軌跡只是滑繩線的一段弧。
滑繩線在滑繩線的方程中，如果l=a(這時 )，方程可約簡為
滑繩線把坐標軸繞原點旋轉180º，x變成-x，y變成-y，方程化為
滑繩線這是環索線方程，所以環索線是滑繩線的特例 。
