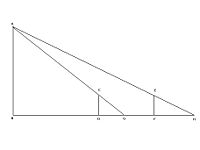
望海島
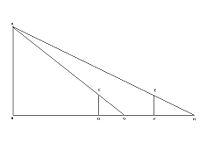 測望法
測望法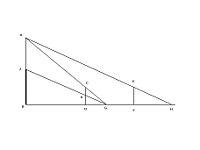 測望法
測望法今有望海島,立兩表,齊高三丈,前後相去千步,令後表與前表三相直。從前表卻行一百二十三步,人目著地取望島峰,與表末三合。
從後表卻行一百二十七步,人目著地取望島峰,亦與表末三合。問島高及去表各幾何? 答曰:島高四里五十五步;去表一百二里一百五十步。 術曰:以表高乘表間為實;相多為法,除之。所得加表高,即得島高。求前表去島遠近者:以前表卻行乘表間為實;相多為法。除之,得島去表里數。
望海島二次測量示意圖
 測望法
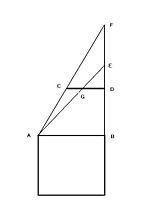
測望法由於前表去島的距離不能直接測量,劉徽用同樣高度的表桿前後測量,表桿與地面垂直,人眼貼地,望表桿頂和島上山頂對齊,這時測得人眼和前表桿的水平距離叫“前表卻行”DF=123步;再將表桿往後移動,兩彪桿間距稱為“表間”=1000步,依法測出“後表卻行”FH=127步。
表高 =CD, 前表卻行=DG 後表卻行=FH 相多=FH-DG 表間=DF 島高=AB 前表去島遠近=BD
依法得島高AB=CDxDF/(FH-DG)+CD
前表去島遠近BD=DGxDF/(FH-DG)
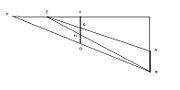
松生山上三次測量示意圖
望松生山上
 測望法
測望法今有望松生山上,不知高下。立兩表齊,高二丈,前後相去五十步,令後表與前表三相直。從前表卻行七步四尺,薄地遙望松末,與表端三合。又望松本,入表二尺八寸。復從後表卻行八步五尺,薄地遙望松末,亦與表端三合。問松高及山去表各幾何? 答曰:松高一十二丈二尺八寸;山去表一里二十八步、七分步之四。術曰:以入表乘表間為實。相多為法,除之。加入表,即得松高。求表去山遠近者:置表間,以前表卻行乘之為實。相多為法,除之,得山去表。
CD EF 表示前後兩支表桿,前表桿有刻度,用作兩次測量,第一次從G點瞄準A、C兩點成直線,第二次從G點校準樹根J,讀出前表桿上度數(入表)。
表高 =CD=2丈 前表卻行=DG=7步4尺 後表卻行=FH=8步5尺 相多=FH-DG 表間=DF=50步 松高=AJ 前表去山遠近=BD 入表=CK=二尺八寸
松高=AJ=CK x DF/(FH-DG)+CK 前表去山遠近=BD=DF x DG/(FH-DG)
南望方邑
今有南望方邑,不知大小。立兩表東、西去六丈,齊人目,以索連之。令東表與邑東南隅及東北隅三相直。當東表之北卻行五步,遙望邑西北隅,入索東端二丈二尺六寸半。又卻北行去表一十三步二尺,遙望邑西北隅,適與西表相三合。問邑方及邑去表各幾何? 答曰:邑方三里四十三步、四分步之三;邑去表四里四十五步。 術曰:以入索乘後去表,以兩表相去除之,所得為景差;以前去表減之,不盡以為法。置後去表,以前去表減之,餘以乘入索為實。實如法而一,得邑方。求去表遠近者:置後去表,以景差減之,餘以乘前去表為實。實如法而一,得邑去表。
由於待測的方城寬度AB,在東西方向,與地面平行,因此兩支在C點D點插入地面與地面垂直的表桿,在此不用作直接測量,測量是依靠一根拴在C、D兩根垂直表桿中間的一條水平測量繩索CD完成的。此題中一根水平測量繩作兩次測量用。
望深谷
今有望深谷,偃矩岸上,令勾高六尺。從勾端望谷底,入下股九尺一寸。又設重矩於上,其矩間相去三丈。更從勾端望谷底,入上股八尺五寸。問谷深幾何?答曰:四十一丈九尺。術曰:置矩間,以上股乘之,為實。上、下股相減,餘為法,除之。所得以勾高減之,即得谷深。
登山望樓
 測望法
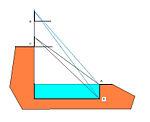
測望法今有登山望樓,樓在平地。偃矩山上,令句高六尺。從句端斜望樓足,入下股一丈二尺。又設重矩於上,令其間相去三丈。更從句端斜望樓足,入上股一丈一尺四寸。又立小表於入股之會,復從句端斜望樓岑端,入小表八寸。問樓高几何? 答曰:八丈。 術曰:上下股相減,餘為法;置矩閒,以下股乘之,如句高而一。所得,以入小表乘之,為實。實如法而一,即是樓高。
南望波口
今有東南望波口,立兩表南、北相去九丈,以索薄地連之。當北表之西卻行去表六丈,薄地遙望波口南岸,入索北端四丈二寸。以望北岸,入前所望表里一丈二尺。又卻後行1去表一十三丈五尺。薄地遙望波口南岸,與南表三合。問波口廣幾何?答曰:一里二百步。 術曰:以後去表乘入索,如表相去而一。所得,以前去表減之,餘以為法;復以前去表減後去表,餘以乘入所望表里為實,實如法而一,得波口廣。
此題中一根水平測量繩,作三次測量用
今有望清淵,淵下有白石。偃矩岸上,令句高三尺。斜望水岸,入下股四尺五寸。望白石,入下股二尺四寸。又設重矩於上,其間相去四尺。更從句端斜望水岸,入上股四尺。以望白石,入上股二尺二寸。問水深幾何? 答曰:一丈二尺。 術曰:置望水上下股相減,餘以乘望石上股為上率。又以望石上下股相減,餘以乘望水上股為下率。兩率相減,餘以乘矩間為實;以二差相乘為法。實如法而一,得水深。又術:列望水上下股及望石上下股,相減,餘為法。以望石下股減望水下股,餘以乘矩間為實,實如法而一,得水深。
A標誌水岸,S標誌白石,C標誌岸邊;句是古代測量用具之一,有兩個邊成直角(如今三角板):使用時句的一邊務必與地面垂直。此題用兩個句,一個在C,一個在D,各測量水岸和水底白石。此題用四次測望術。
登山望津
今有登山望津,津在山南。偃矩山上,令句高一丈二尺。從句端斜望津南岸,入下股二丈三尺一寸。又望津北岸,入前望股里一丈八寸。更登高岩北,卻行二十二步,上登五十一步,偃矩山上。更從句端斜望津南岸,入上股二丈二尺。問津廣幾何? 答曰:二里一百二步。 術曰:以句高乘下股,如上股而一。所得以句高減之,餘為法;置北行,以句高乘之,如上股而一。所得以減上登,餘以乘入股里為實。實 如法而一,即得津廣。
登山臨邑
今有登山臨邑,邑在山南。偃矩山上,令勾高三尺五寸。令勾端與邑東南隅及東北隅三相直。從勾端遙望東北隅,入下股一丈二尺。又施橫勾於入股之會,從立勾端望西北隅,入橫勾五尺。望東南隅,入下股一丈八尺。又設重矩於上,令矩間相去四丈。更從立勾端望東南隅,入上股一丈七尺五寸。問邑廣長各幾何? 答曰:南北長一里一百步;東西廣一里三十三步、少半步。術曰:以勾高乘東南隅入下股,如上股而一,所得減勾高,餘為法;以東北隅下股減東南隅下股,餘以乘矩間為實。實如法而一,得邑南北長也。求邑廣:以入橫勾乘矩間為實。實如法而一,即得邑東西廣。
此題用四次測望術
註:《海島算經》共九問。從題目文字可知所有計算都是用籌算進行的。“為實”指作為一個分數的分子,“為法”指作為分數的分母。所用的長度單位有里、丈、步、尺、寸;1里=180丈=1800尺;1丈=10尺:1步=6尺,1尺=10寸。