定義
靜止流體不能承受剪應力，因而流體作用於邊界面元上的力必須與這些面元垂直。 考慮流體內部的一個小體積元，其上、下面積為dA，高為dz（見圖2），
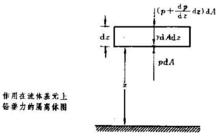圖2 作用在流體基元上鉛垂力的隔離體圖則體積元下面的作用力為pdA，上面的作用力為
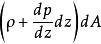流體靜力學由平衡條件可得：
dp=－γdz=－ρgdz （1）
式中γ為流體比重；ρ為流體密度；g為重力加速度。對於液體，ρ基本上是常數，積分上式可得：
p=p+ρgh
式中p為液體內部某點的壓力；h為該點距液體自由表面的深度；p為自由表面上的壓力。用此公式可計算各種液體在不同深度處的壓力。
對於氣體，為了積分方程（1），必須給出ρ隨壓力或高度的變化。在對流層中，溫度隨高度線性下降，即
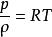流體靜力學T=T－βz，式中T為地球表面z=0處的熱力學溫度；β為比例常數。大氣的壓力p與密度ρ之間服從狀態方程，式中R=287.14米/（秒·開），為氣體常數。
故有：
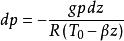流體靜力學（2）
積分式（2）可得出大氣中任意高度z處的壓力和密度的公式：
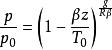流體靜力學
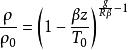流體靜力學式中p、ρ為z=0處的壓力及密度值。在同溫層中，式（1）給出下述壓力、密度隨高度的變化關係：
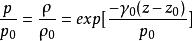流體靜力學式中p和γ是p與γ在高度z處的值。
研究的基本問題
流體靜力學主要研究下列基本問題：
靜止液體內的壓力（壓強）分布，壓力對器壁的作用，分布在平面或曲面上的壓力的合力及其作用點，物體受到的浮力和浮力的作用點，浮體的穩定性以及靜止氣體的壓力分布、密度分布和溫度分布等。
從廣義上說，流體靜力學還包括流體處於相對靜止的情形，例如盛有液體的容器繞一垂直軸線做勻速旋轉時的自由表面為旋轉拋物面就是一例。
套用
人們在航空飛行，設計水壩、閘門等水工結構以及液壓驅動裝置和高壓容器時，都需要套用流體靜力學的知識。
