流體運動學

從幾何學觀點研究流體運動所遵循的規律的流體力學分支，流體質點運動的軌跡稱為跡線。

流體運動學

正文

從幾何學觀點研究流體運動所遵循的規律的流體力學分支。
描述流體運動的方法　描述流體運動有兩種方法。①拉格朗日法：通過描述每一個流體質點物理量（如速度、壓力等）隨時間的變化來研究流體的運動。②歐拉法：通過描述流場（充滿流體的空間）中各個時刻每一個空間點上的物理量來研究流體的運動。歐拉法中物理量B表示為空間點位置和時間t的函式，即B=B(x、y、z、t)。如流場中所有空間點上的各個物理量均不隨時間變化，即，這種流動稱為定常流動,否則就是不定常流動。
跡線、流線和流管　流體質點運動的軌跡稱為跡線。在給定時刻，沿流場中每一點的速度方向作一微小線段，這些線段的連線構成一簇曲線，它們中的每一條曲線都稱為流線。因此，流線上任意一點的切線方向就是該點流速方向。流線可以隨時間而變，但定常流動時流線不隨時間變化，且與跡線重合。流動中任取一條不是流線的封閉曲線，通過該曲線的所有流線構成一個管狀曲面稱為流管（見圖）。流管表面沒有流體通過，流體只能在流管中流動。流體沿管道流動時，管壁也是流管。對於不可壓縮流體，流管中體積流量保持不變。如果流管橫截面積A縮小，則平均流速v增大，反之，則平均流速減小。

流體運動學

質點導數　流體質點物理量隨時間的變化率。如用B表示某物理量，則其質點導數表示為。在歐拉法中其展開式為

式中v為速度向量；墷B為物理量 B的梯度。稱為物理量B的當地導數或局部導數，v·墷B 稱為物理量 B的遷移導數或對流導數，稱為質點導數運算元。根據上式，在歐拉法中，流體質點加速度（即速度的質點導數）。在直角坐標系中，分別用v=u i+v j+w k,u、v、w和i、j、k表示x、y、z方向的速度分量和單位，則

流體微團速度分解定理　流體微團的運動可以分解為平移、剛體轉動和變形運動，微團上任意兩點間的相對速度可以看成是由剛體轉動和變形運動構成的。
無鏇流動和有鏇流動　流場中渦量處處為零的流動稱為無鏇流動，否則就是有鏇流動。渦量（Ω）就是速度的鏇度,它等於流體微團剛體鏇轉角速度ω的2倍，反映流體微團鏇轉的快慢和方向。在直角坐標系中，

速度勢　無鏇流動時存在速度勢墷嗞，它與速度的關係為v=墷嗞，在直角坐標系中表示為

運動學邊界條件　流體在邊界上必須滿足運動學條件。對於粘性流體，在與固體交界時，界面上任一點的速度等於該點上流體質點的速度;在分層流體邊界上,界面兩側流體質點的速度彼此相等。對於無粘性流體，在與固體交界時，界面上任一點的法向速度等於該點上流體質點的法向速度；在分層流體邊界上，界面兩側的流體質點永遠保持在邊界面上。
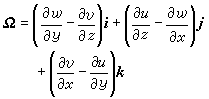
參考書目
　G.K.Batchelor,An Introduction to Fluid Dynamics,Cambridge Univ.Press,Cambridge,1970.

配圖

相關連線