牛頓三大定律
牛頓三大定律是力學和運動學等的基礎。物質構成和狀態都要用到牛頓三大定律。牛頓三大定律還有很多套用。它能為以下結論作出很多合理解釋。
伯努利原理
飛機運動時,機翼前大後小,機翼以它的最大截面並沿運動方向切割空氣,並在機翼尾部和機翼後方形成一定真空。由於流體向各個方向都有壓強,機翼尾部形成真空的四周空氣受到大氣壓的作用而加速運動,這些空氣到達機翼尾部就有一定的延時。飛機運動中,機翼的形狀決定了,空氣尾部的下面空氣先對機翼產生壓力作用,機翼的上面沒有空氣作用或有部分空氣作用,這樣就形成了壓力差,產生了升力。飛機運動時,我們分清了氣壓對氣體和飛機產生的許多作用。我們才能更好地理解伯努利原理。換句話說,飛機的重力可以用來改變飛機的運動方向或對空氣分子加速等。
足球表面存在凹面,足球旋轉並向前運動時,足球沿運動方向切割空氣。足球前進並順時針方向旋轉時,它的凹面帶動空氣一起運動,並在空氣阻力作用下,上方空氣速度減小,下方空氣速度增加。空氣有速度差,空氣速度越大產生的排空效應就越強,形成的真空範圍越大,延時越長,氣壓能作用於球的壓力越小。
固體管道能隔絕外界氣壓等,固只需要管道中流體的兩頭壓強相等。固體管道中,流體的動量也能產生壓強。流體的能量守恆等推導出伯努利方程。伯努利方程適用於固體管道中流動的理想流體。單純地說:在水流或氣流里,如果速度小,壓強就大,如果速度大,壓強就小。這樣的說法就是很牽強的說法。
理想氣體狀態方程
理想氣體狀態方程是由研究低壓下氣體的行為導出的。但各氣體在適用理想氣體狀態方程時多少有些偏差;壓力越低,偏差越小,在極低壓力下理想氣體狀態方程可較準確地描述氣體的行為。極低的壓強意味著分子之間的距離非常大,此時分子之間的相互作用非常小;又意味著分子本身所占的體積與此時氣體所具有的非常大的體積相比可忽略不計,因而分子可近似被看作是沒有體積的質點。於是從極低壓力氣體的行為觸發,抽象提出理想氣體的概念。
實際氣體都不同程度地偏離理想氣體定律。偏離大小取決於壓力、溫度與氣體的性質,特別是取決於氣體液化的難易程度。當溫度較低、壓力較高時,各種氣體的行為都將不同程度地偏離理想氣體的行為。此時需要考慮分子間的引力和分子本身的體積重新構造氣體狀態方程。氣體之間的作用力不計時,我們認為氣體分子沒有產生堆積。極低的壓強意味著分子之間的距離非常大,重力作用於分子而沒有其它力平衡分子重力,在這段距離內,重力使分子加速運動,產生動量,這些動量在單位時間和面積內就能產生壓強。極低的氣壓意為著氣體分子之間有比較大的距離,我們認為分子重力主要是通過動量傳遞的。氣體的動量和溫度、物質的量等有關係,兩個多世紀以來許多科學家經過不斷地試驗、觀察、歸納總結,得出了理想氣體狀態方程。分子間的作用力很小,加上溫度較高、壓力較低時,進一步削弱分子力的作用;壓強較低,又能忽略分子本身體積。這樣的氣體就接近理想氣體。
滲透壓
了解了物質的三態和理想氣體狀態方程,我們能更好的理解滲透壓。如果滲透壓是溶質微粒對水的吸引力。那么溶質微粒對水的吸引力越大,滲透壓就應該越大 。顯然情況不是這樣的,溶質微粒對水的吸引力的大小與滲透壓大小無關。意為著滲透壓需要一個更為合理的解釋。
膠體、溶液和懸濁液受浮力和重力外,還受分子作用力等的影響。同一溶器中,膠體和溶液的溶質與溶劑濃度的比值幾乎不變的原因,除了浮力的作用,還有擴散力和分子作用力(分子作用力包括液體張力)等的作用。溶液中,由於溶質和溶劑產生的重力不一樣,形成的物質堆積(參照密堆積結構)有一定形變。張力平衡溶質和溶劑的重力差。擴散又使溶質能分散於溶劑之中。
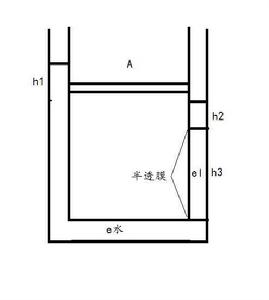
 流體永動機
流體永動機氣液交接面:空氣與水的交接面,它的壓強比較高,氣體濃度高,但不足以阻止高濃度的水分子擴散。水分子間的吸引力較大,彼此之間產生引力疊加,加上有一段距離(此距離內,分子動量克服分子間引力和本身重力做功),分子能產生劇烈的濃度分布,直到壓力、分子重力和引力的合力與分子斥力相等。此時,保守力場的合力為零。即有擴散力各向同性,擴散力合力為零。壓力、引力、分子靜電力和分子的擴散力的整體作用力的作用效果的合力為零。當然,局部範圍和時間內,合力可以不為零。液體內擴散力產生的壓強處處相等,即有等式C1R1T1=C2R2T2。液體中,液體的濃度和溫度隨壓強的增加而增加,常數R隨壓強的增加而減小。固化和液化的難度隨壓強增加而減小。
麥克斯韋-玻爾茲曼分布可以用統計力學來推導(參見麥克斯韋-玻爾茲曼統計)。它對應於由大量不相互作用的粒子所組成、以碰撞為主的系統中最有可能的速率分布,其中量子效應可以忽略。由於氣體中分子的相互作用一般都是相當小的,因此麥克斯韋-玻爾茲曼分布提供了氣體狀態的非常好的近似。 液體和固體是具有很強的量子效應。可以認為液體和固體中,不存在麥克斯韋-玻爾茲曼分布中的分子速率分布;但存在電子的速率分布。
液體和固體分子是堆積起來的物質。分子的壓力和重力的傳遞是依靠分子間的作用力。根據力學平衡可知:分子的動量相互抵削,合力為零。(若分子的動量產生的合力不為零,則分子會發生相對移動,直到合力為零為止。)註:力學平衡表明,液體和固體的平均振動壓強不變,隨著重力的增加,分子濃度和分子的電子的靜電勢能增加,分子的平均振動能減小,輻射能增加。
因為平衡滲透壓遵循理想氣體定律。所以滲透壓是很多力作用的結果。
永動機原理
熱力學第二定律是建立在對實驗結果的觀測和總結的基礎上的定律。雖然在過去的一百多年間未發現與第二定律相悖的實驗現象,但始終無法從理論上嚴謹地證明第二定律的正確性。自1993年以來,Denis J.Evans等學者在理論上對熱力學第二定律產生了質疑,從統計熱力學的角度發表了一些關於“熵的漲落“的理論,比如其中比較重要的FT理論。而後G.M.Wang等人於2002在Physical Review Letters上發表了題為《小系統短時間內有悖熱力學第二定律的實驗證明》。從實驗觀測的角度證明了在一定條件下熱,孤立系統的自發熵減反應是有可能發生的。
如圖所示:一部分人認為麥克斯韋-玻爾茲曼分布——溶液隨深度的增加,溶質、溶劑濃度增加。意味著熱溶質的滲透壓增加,滲透壓能抵消溶液密度大於水的密度所產生的壓強差。這樣永動機就不成立。依照這部分人的說法,溶液密度小於溶劑水的密度,溶質的濃度隨深度增加而增加。此時,滲透壓能加大溶液與水的密度差而產生的壓強差。這樣永動機就成立。顯而易見,這部分人的說法是不正確的。熱力學第二定律是在一定條件下得出的結論。它和流體永動機沒有交集。因為熱力學第二定律推出不存在永動機的結論是不夠嚴謹的結論。所以永動機的存在與否有爭議。
綜上所述:保守力場重力能與分子力相互抵消。根據牛頓三大定律和實際氣體的知識等可知,液體分子的擴散力的合力為零。即溶液中,溶質的滲透壓處處相等。
圖中,在連通器中,流體產生的力和所受的力具有一定的對稱性。也就是說流體產生的力和所受的力的合力為零。從相對論的等效原理中可知:水溶液和水的密度差產生了壓強差(e1-e2)gh3。假設半透膜的面積是S;流體永動機的輸出壓強是PS;流體所受的流體阻力是kv。力學平衡和能量守恆等知識有:溶質擴散增加的重力勢能與減少的重力勢能(減少的重力勢能是一部分轉化為其它形式的能,另一部分克服摩擦力做功)相等。也就是壓強差(e1-e2)gh3產生的勢能分成相等的兩部分。即1/2(el-e水)v^2S=1/2(el-e水)gh3S=PS+kv小於擴散產生的壓強nRT/V。又因為伯努利方程(濃度和面積不變,意為著濃度和流量不變)。擴散所受的阻力是f。簡化有:公式1/2(e1-e2)Sv^2+PS+kv+0和nRT/V=1/2(el-e水)v^2+f/S。即如圖所示具有一定結構的連通器的流體永動機能產生一定的輸出功率。
題外話:氣體分子的作用力(張力和氣體的吸附力等)、氣體的擴散、汽車的攪動和氣體的浮力是霧霾產生的原因。汽車尾氣的吸附力產生大顆粒物質。氣體的擴散、汽車的攪動和氣體的浮力增加大顆粒物質的產生速度並延長大顆粒物質在空氣的停留時間,形成霧霾。