簡介
 波浪破碎
波浪破碎中文名稱:波浪破碎
英文名稱:wavebreaking
所屬學科:水利科技(一級學科);水力學、河流動力學、海岸動力學(二級學科);海岸動力學(水利)(三級學科)
波浪破碎是個古老而全新的課題,在規則波方面,將已有的研究方法歸為三類:涌模型、表面水滾模型和紊流模型。經分析認為:紊流模型和表面水滾模型適用於崩破情況,而涌模型對崩破及卷破都有很好的適用性。通過底坡度為1/45、1/30和1/15三種坡形的物理模型試驗結合涌模型理論,找到破碎係數和破碎類型參數之間的經驗關係。和其他學者的研究成果對比表明,
在不規則波方面,將已有的研究不規則波破碎模型分為兩類:參數法和機率法。不規則波試驗分析表明:波浪破碎前,波高分布可用格魯霍夫斯基分布很好地表示;在破碎帶及破後形成的穩定波列的波高都可由瑞利分布很好地代表。本論文通過分析試驗數據,得到了破碎機率經驗曲線,試驗結果對比表明,該機率曲線能很好地代表近岸波浪的破碎特性。
特點
 波浪破碎
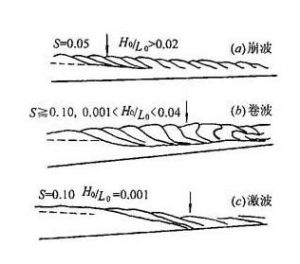
波浪破碎當風浪成長過程波陡達到極限狀態或波浪在淺水區傳播受水底邊界影響,剖面發生顯著變形,波峰水質點水平分速達到或超過波速,使波浪發生破碎的現象。這時的波浪稱為破波。因水底坡度和波陡的不同,破波可分為崩波(spillingbreaker)、卷波(plungingbreaker)和激波(surgingbreaker)三種。
波陡較大的波浪沿緩坡傳播時發生崩波,首先在波峰頂出現浪花逐漸擴大到波峰前坡,整個波形仍基本上保持對稱,傳至岸線附近時波峰前坡布滿泡沫,最後波浪消失在岸坡上。波陡較小的波浪在較陡的底坡上傳播時發生卷波,波峰前坡逐漸陡直,終於整個波峰捲曲形成水舌而傾倒破碎,空氣被捲入水體而發生轟鳴,波形發生明顯變形失去對稱。波高較小的長波在較緩的底坡上傳播時產生激波,波峰變陡後從其前坡下部開始出現浪花並擴大到整個前峰面,呈激散破碎隨波峰推帶著前進,最後與波峰一起破散在岸灘上。
波浪破碎引起水體的紊動,損耗大量波能,是近岸泥沙運動、岸灘沖刷的重要動力因素。蒙克(Munk)根據孤立波理論推得破波的極限波高(稱破碎波高)Hb和破碎水深(又稱臨界水深)db的關係:Hb=0.78db。米徹爾(Michell)根據斯托克斯波理論:當波陡達到極限值時,峰頂水質點的水平分速與波速相等,峰頂發生破碎,導得破碎時的極限波陡。
相關研究
一、綜述
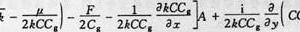 波浪破碎
波浪破碎波浪從深水向淺水傳播過程中,由於淺化變形,會在海岸附近發生波浪破碎.波浪破碎過程中將伴隨大量的能量損失,導致波高等波要素髮生很大變化,從而在近岸區域出現明顯的增成水現象。
自20世紀60年代以來,許多學者採用物理模型實驗和數學模型對波浪增減水現象進行了研究,取得了許多重要研究成果,但由於該現象的複雜性,目前對波浪增減水的模擬大多是先採用考慮能量損失的波能平衡方程得到波高分布,接著採用Longuet-Higgins和stewart原始輻射應力公式或其簡化公式計算輻射應力分量,最後採用深度平均的方程計算平均水位的變化(增減水)。
 波浪破碎
波浪破碎對簡單地形,這種方法是十分有效的,但對複雜地形這種方法存在明顯不足,主要表現在:(1)考慮能量損失的波能平衡方程在用於二線問題時,需要採用其他方程計算波向,而複雜地形上的波向的求解十分困難,特別在焦散區附近更是如此;(2)直接採用Longuet-Higgins和Stewat原始公式計算輻射應力分量比較複雜,需要採用其他方程得到波浪水質點的速度、壓力及波面分布,其簡化公式只適用於簡單的純行進波,而且仍需採用其他方程計算出各點的波向,從而使這種比較常用的波浪增減水模型算法在複雜地形上的套用受到限制.為此,本文給出一種比較實用的波浪增減水數學模型.該模型首先採用考慮能量損失的拋物型緩坡方程得到域內的波浪復振幅分布,避免了波向的確定,接著採用筆者導出的一種新的輻射應力公式計算出輻射應力分量,最後採用深度平均的方程計算波浪破碎產生的增減水.從理論上說,本文方法可有效地用於複雜地形上的增減水問題,但由於缺少複雜地形上的增減水實測數據,因此模型的驗證是在簡單地形上進行的.採用該模型對規則波和不規則波破碎引起的增減水問題進行了數值模擬,並將數值結果和實測數據進行了比較,效果比較滿意。
 波浪破碎
波浪破碎二、數學模型
1、波浪復振幅數學模型。
考慮波能損失的拋物型緩坡方程為
式中,A為波浪復振幅;X為波浪主傳播方向;k為波數;為縱軸方向(y方向)上k的平均值;C為波相速;Cg為波群速;μ為非線性因子,可由Kirby和Dalrymple提出的非線性頻散模型確定;F=(Df+Db)/E,為能量損失因子,E=pg|A|2/2,為波能,Df和Db分別為底摩擦和波浪破碎引起的能量損失,可採用下面的公式進行計算:
其中p為密度;ƒw為底摩擦係數,可由經驗公式確定;w為波浪圓頻率;H為波高;h為靜水深;g為重力加速度;a1為校正係數(≈);ƒp為不規則波譜峰頻率;Qb和Hb分別為不規則波當地破波分數和最大破波波高,它們分別由下面的表達式確定:
 波浪破碎
波浪破碎其中kp為譜峰頻率對應的當地波數;r為破波參數,可由經驗公式r=0.5+0.4tanh(33So)或實際增況確定,So為初始人射波陡。
2、輻射應力計算公式
由推導拋物型緩坡方程(1)所做的簡化假定,並將輻射應力分量與式(1)中的待求變數聯繫起來,可以導出下面的輻射應力分量計算公式:
式中,Sxx,Syy,Sxy和Syx為輻射應力分量;A為A的共扼複數;其他變數含義同前.當套用武(1)計算出計算域中各點的復振幅A後,採用式(2)可十分容易地計算出各點的輻射應力分量。
三、波浪增減水數學模型
對波浪增減水採用深度平均的連續方程和動量方程進行計算,具體表達式如下:
式(1)一(3)構成了複雜地形上的波浪增減水數學模型。但對本文算例,可採用式(4)代替式(3)進行簡化計算。
式(1)採用Crank-Nicolson格式離散,並結合適當的邊界條件採用追趕法進行求解,就得到計算域中復振幅A(x,y)的分布;將A(x,y)代入式(2),可十分容易地計算出域中各點的輻射應力分量,然後將輻射應力分量代人式(4)即可可求出η值.在本文計算中,式(2)和(4)中的一階導數均採用中心差分格式離散。
 波浪破碎
波浪破碎四、數學模型的驗證及結果分析
1、規則波破碎引起的波浪增減水
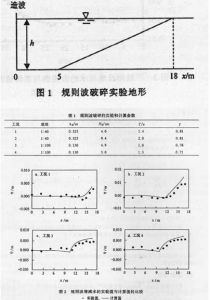
進行的規則波破碎的物理模型實驗結果來驗證本文給出的波浪增減水數學模型.其實驗地形如圖1所示.有關實驗和計算採用的參數如表1所示,其中ho為造波位置的靜水深,Ho為人射波高,T為周期,r為破波參數.圖2給出了四種工況的波浪增減水的實驗值和計算結果的比較,可以看出兩者比較一致,初步說明本文給出的沾染增減水數學模型比較成功的。
2、不規則波破碎引起的波浪增減水
這裡對一種典型地形上不規則波破碎引起的波浪增減水進行數值模擬,在該地形上
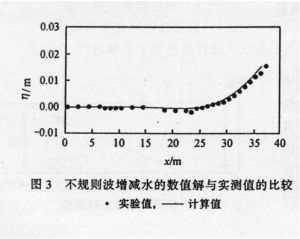
Sitve進行了不規則波破碎的物理模型實驗,其實驗結果被一些學者用來驗證數學模型.有關實驗參數和計算參數如表2所示,其中Hrmo為人射位置的不規則波的均方波高,ƒp為譜峰頻率,其他參數同表1.圖3給出了波浪增減水的計算值與實測結果的比較,可以看出兩者相當一致,這進步說明本文模型是比較有效的。
波浪增減水是近岸區波浪破碎引起的一種比較常見的現象,針對現有模型存在的問題,提出了一種模擬近岸區波浪增減水的實用數學模型.採用該模型對規則波和不規則波破碎引起的增減水進行了數值模擬,數值結果與實驗數據的比較表明,該模型可有效模擬近岸區的波浪增減水現象。
生活中的自然現象
| 人的意識也是以自然方式發生的物質世界。人和人的意識是自然界發展的最高產物。物質世界具有系統性、複雜性和無窮多樣性。它既包括人類已知的、也包括人類未知的物質世界。讓我們一起走進自然吧~~ |
