引言
最最佳化理論的發展之一是wolpert和Macerday提出了沒有免費的午餐定理(No Free Lunch，簡稱NFL)。該定理的結論是，由於對所有可能函式的相互補償，最最佳化算法的性能是等價的。該定理暗指，沒有其它任何算法能夠比搜尋空間的線性列舉或者純隨機搜尋算法更優。該定理只是定義在有限的搜尋空間，對無限搜尋空間結論是否成立尚不清楚。
NFL定理
1）對所有可能的的目標函式求平均，得到的所有學習算法的“非訓練集誤差”的期望值相同；
2）對任意固定的訓練集，對所有的目標函式求平均，得到的所有學習算法的“非訓練集誤差”的期望值也相同；
3）對所有的先驗知識求平均，得到的所有學習算法的的“非訓練集誤差”的期望值也相同；
4）對任意固定的訓練集，對所有的先驗知識求平均，得到的所有學習算法的的“非訓練集誤差”的期望值也相同。
NFL定理表明沒有一個學習算法可以在任何領域總是產生最準確的學習器。不管採用何種學習算法，至少存在一個目標函式，能夠使得隨機猜測算法是更好的算法 。
NFL理論詳解
沒有免費午餐定理首先，假設一個算法為a，而隨機胡猜的算法為b，為了簡單起見，假設樣本空間為 和假設空間為H都是離散的。令P(h|X,a)表示算法a基於訓練數據X產生假設h的機率，再令f代表希望的真實目標函式。a的訓練集外誤差，即a在訓練集之外的所有樣本上的誤差為
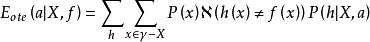沒有免費午餐定理
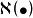沒有免費午餐定理
沒有免費午餐定理其中 是指示函式，若 為真則取值1，否則取值0.
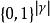沒有免費午餐定理
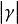沒有免費午餐定理
沒有免費午餐定理 沒有免費午餐定理考慮二分類問題，且真實目標函式可以是任何函式 ↦{0,1},函式空間為 (指樣本空間中元素個數，對所有可能的f按均勻分布對誤差求和，有
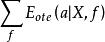沒有免費午餐定理
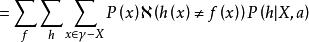沒有免費午餐定理
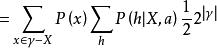沒有免費午餐定理
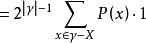沒有免費午餐定理可以看到總誤差竟與算法無關，對於任何兩個算法a和b都有
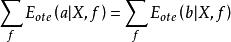沒有免費午餐定理所以，NFL定理最重要意義是，在脫離實際意義情況下，空泛地談論哪種算法好毫無意義，要談論算法優劣必須針對具體學習問題。
