決策論

根據系統的狀態信息和評價準則選取最優策略的數學理論。決策論是運籌學的一個分支和決策分析的理論基礎。決策論是根據信息和評價準則，用數量方法尋找或選取最優決策方案的科學，是運籌學的一個分支和決策分析的理論基礎。在實際生活與生產中對同一個問題所面臨的幾種自然情況或狀態，又有幾種可選方案，就構成一個決策，而決策者為對付這些情況所取的對策方案就組成決策方案或策略。

效用理論　效用理論是決策論的基礎。事物的不確定性可看作是許多簡單隨機事件的複合。每一個簡單隨機事件是由兩個互斥事件a1與a2組成的。事件 a1發生的機率為P，事件 a2發生的機率為1－P，則隨機事件記作L(a1,P, a2)。在簡單隨機事件的集合內引進“優先”或“偏好”的概念。並在此隨機事件集合的基礎上建立公理體系，即假設在隨機事件集合中存在下列條件：①相對偏好順序；②偏好關係具有可傳遞性；③簡單隨機事件間的可比性；④偏好可以量化；⑤不確定性判斷可以量化；⑥等價隨機事件可互相代換。在這樣的條件下可用一個數值來描述簡單隨機事件的期望效益，稱為效用。由簡單隨機事件的效用可確定一般不確定事件的效用。在對事件不確定性判斷進行量化時，需要利用各種知識，如系統本身的特性，一些必要的統計知識，以及決策者根據經驗對事件不確定性的主觀估算等。
決策樹　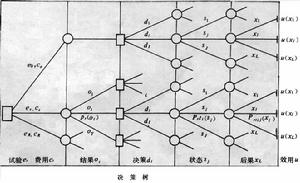決策論中最常用的方法之一是決策樹方法。下圖為典型的決策樹。圖中的長方形小框表示由人選擇的決策點。把需要作決策的問題過程畫成示意圖，由圖的最左邊出發,在作決策之前先作試驗。例如由R個試驗中選取試驗er，費用為cr,試驗結果有o1,…,ot,…,oT等共 T個。 在試驗 er條件下結果 ot 發生的機率記為Pr(ot)。設此時有d1，…，di,…,dI等共I個備選決策方案。若選擇決策di,則這時可能出現s1,…,sj,…,sJ共J種狀態。在試驗er中出現結果ot時選取決策di的條件下,狀態sj出現的機率記作Prtij(sj)。此時可能有L種後果x1,…，xl,…,xL，而Prtij(xl)表示在試驗er中出現結果ot時，選取決策di而出現狀態sj的情況下,發生後果xl的機率，其效用記作 u(xl)。圖中e0表示不作試驗的情況。決策樹的方法是順著樹的各個分枝進行分析，並計算各種可能情況的機率的大小，最後計算在這些條件下最終出現的後果的效用，將各種效用加以比較，從中選取最佳效用所對應的試驗與決策作為應取的決策。
貝葉斯決策　由於決策總是在事件發生之前作出，而事件是否發生又是不確定的，因此常採取統計學中貝葉斯公式對事件發生的機率作先驗估計，這就是貝葉斯決策方法。
由於事件的發生具有不確定性，這就使決策帶有一定的風險性。人們對於風險的態度不同，對效用的估計也不同。對事物發展持保守看法而不願冒險的人，對效用估計往往偏低；傾向於冒險的人，對效用的估計往往偏高。也有人取中庸態度，對效用的估計介於兩者之間。