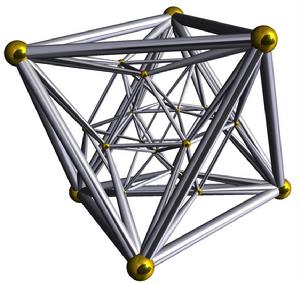
簡介
它的施萊夫利符號為{3,4,3}，自身對偶
其頂點圖是立方體，正24胞體每條棱上有3個正八面體。
三維投影
施萊格爾投影
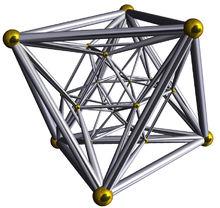施萊格爾投影嚴格來說正二十四胞體是沒有三維類比的，因此也不好說是根據哪個正多面體的施萊格爾投影類比到三維上來的。
不過只要根據正二十四胞體每條棱上有3個正八面體這個條件在三維空間上畫投影就不會太難，如右圖。
正二十四胞體的構成數據如下：
球極投影胞（正八面體）數：24，面（正三角形）數：96，棱數：96，頂點數：24
球極投影
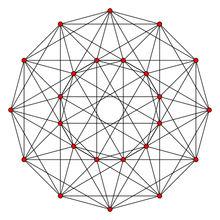二維線架投影將正二十四胞體的表面膨脹使之成為一個超球，然後投影到三維上，如左圖。
二維線架正投影
如右圖，有線段重合。
以(±1,±1,0,0)的全排列為頂點坐標建立正二十四胞體，進行正交變換
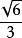正二十四胞體
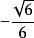正二十四胞體 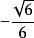正二十四胞體（，，， 0
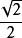正二十四胞體
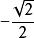正二十四胞體0 ，，， 0
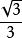正二十四胞體 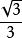正二十四胞體 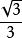正二十四胞體，， ， 0
0， 0， 0， 1）
向前兩坐標所在平面投影可得此圖。
也可以將此正二十四胞體投影至前三坐標軸所在三維空間投影，再作此投影的正軸測圖，也得到此二維線架正投影。
施萊夫利符號
正二十四胞體24-cell的施萊夫利符號有好幾個 {3,4,3}：特指它是正多胞體Icositetrachoron
t1{3,3,4}（t後面的那個“1”下標）：特指它由16-cell截角得到，代指Rectified 16-cell
t1{3^(1,1,1)}（t後面的那個“1”下標，“1,1,1”上標）：特指它由Demitesseract截角得到，代指Rectified demitesseract
類比
也不能說沒有三維類比，畢竟正方形是24-cell的二維類比，在根據它們兩個的施萊夫利符號，一定意義上說正二十四胞體還是有三維類比的：截半立方體（半正多面體）或菱形十二面體（卡塔蘭立體，半正多面體的對偶） 同時正二十四胞體不會有向更高維的類比
二胞角
對於的二胞角的求導是要用到四維解析幾何慢慢求的，太麻煩，這裡有種特殊的方法
因為正十六胞體的二胞角是120°，因此可以用它做一個四維空間堆砌(Tetracomb)，每個面上有三個正十六胞體——即施萊夫利符號為{3,3,4,3}，得到這個堆砌的對偶{3,4,3,3}——同樣是一個四維空間堆砌，而這個對偶每個面上有三個正二十四胞體（{3,4,3}），所以正二十四胞體的二胞角和正十六胞體一樣是120°。
坐標
正二十四胞體的24個點坐標有點特殊，是一個超正方體與一個正十六胞體的結合：前16個點坐標是(±0.5,±0.5,±0.5,±0.5)，後8個點坐標是(±1,0,0,0)的全排列。另一方面24個點坐標也可以(±1,±1,0,0)的全排列
因為正二十四胞體的那四項數據(24,96,96,24)均是超正方體與正十六胞體的各項和，所以又稱：
超正方體+正十六胞體=正二十四胞體
