基本分類
正五胞體
正五胞體(Pentachoron,5-cell),又作正四面體錐(hyperpyramid),4-單形(4-simplex),是正多胞體中最簡單的一個。
簡介
其施萊夫利符號是{3,3,3},頂點圖(Vertex figure)是正四面體,在正五胞體中每條棱上有三個正四面體
一般而言,它是正四面體的四維類比
施萊格爾投影
把正四面體的投影類比到正五胞體 的三維投影上來:
首先在外面做一個正四面體框架,然後找到它的幾何中心定一個點,再將這個點向“外面”的四個點連上線,如右下圖。
 正多胞體
正多胞體但看到這個圖你可能不理解這是個什麼東西,實際上這只是一個三維的投影(圖片嘛,又要把這個三維投影再投影到二維上),正五胞體在我們這個三維世界上是不存在的,但是我們仍然可以去理解,理解四維空間的種種奇特之處。
右圖確確實實是表現了正五胞體的三維投影,但實際上它不是平行投影來的,這種投影叫“施萊格爾投影”,是在它的外接球(四維的是外接一個“超球”)上取一點作的透視投影——這個施萊格爾投影的“內部”的那一點看上去比外面四個點明顯要小一些。
算上“最外部”的那個四面體,正五胞體一共由五個正四面體組成,也就是有五個“胞”(cell,指組成高維多胞形的三維表面),之後我們就得到正五胞體的一些數據
胞(正四面體)數:5,面(正三角形)數:10,棱數:10,頂點數:5
球極投影
將一個多面體的表面不斷膨脹,可以讓它的所有表面變成球面。變成一個球後再將球面投影到無窮大的平面上,這就是二維球極投影(如圖)
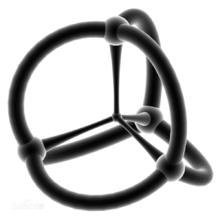 正多胞體
正多胞體同樣,四維的物體也可以通過球極投影把它的三維表面展現在三維上
。將正五胞體的三維表面不斷向它的外部膨脹變成“超球”,再把超球的表面投影進平坦的三維空間。
右圖就是正五胞體的三維球極投影,和施萊格爾投影一樣,投影中心的那個點實際上比外面四個點要小一點。
二維線架正投影
四維的正五胞體可以不經過三維而直接投影到二維上,但只能表現一些點與線之間的連線關係,如下圖
。
實話說這個投影是怎么寫入五個點的坐標投影得到的,不過這不重要,作為四維單形的正五胞體就是這么“簡單”,作一個正五邊形,每兩點兩兩連線,這就是它的二維線架正投影(沒錯,是正的)
一個四維物體的二維正投影其實不止一種的,不同的投影用來抽象表現這個東西不同的特性,正五胞體的二維投影英文維基上有很多,但為了表現那些特性,或多或少都有幾條線段重合,這裡略去。
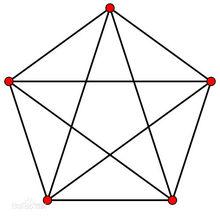 正多胞體
正多胞體與單形有聯繫
正八胞體(超正方體)
正八胞體,在幾何學中四維方體是立方體的四維類比,四維方體之於立方體,就如立方體之於正方形,四維方體是四維凸正多胞體,有8個立方體胞,立方體維數大於3推廣的是超立方體或測度多胞體。
簡介
其施萊夫利符號是{4,3,3}
超立方體,又作正八胞體 (8-cell,Regular octachoron),立方體柱(Cubic prism),4-4邊形柱(4-4 duoprism),是一個四維空間裡的幾何產物。
需要說一下“超立方體”的英文應該是Tesseract而不是Hypercube,Hypercube在英文維基百科上是指N維立方體(一維的線段,二維的正方形,三維的立方體……)的總稱。
施萊格爾投影
 正多胞體
正多胞體對於生活在三維空間的人類來說,四維世界是很神秘的概念。正像生活在二維世界裡的小人(如果存在)很難想像三維世界一樣,我們同樣難於想像四維世界。不過也正像我們可以通過研究三維物體在二維物體上的投影來研究想像三維物體一樣,我們也可以通過四維物體在三維世界中的立體圖形投影來研究四維世界。
如圖所示的是一個立方體在二維世界中的投影。二維小人多多少少可以通過這些投影來想像那個“三 維立方體”的神秘圖形。他們可以數出這個立方體有8個頂點,12條邊,6個面。可以看到圖1的樣子像是一個大正方形套一個小正方形,那我們用一點類比的思維,把一個大立方體“套住”一個小立方體,這就得到一個超正方體的一種三維投影(當然圖2又是它的二維投影)在二維世界裡(不考慮時間軸)要把不透明圖形簡化的只有頂點(二維物體中的零位框架)之後二維(如果存在)小人才能看得到內部,在我們在三維世界裡要簡化到凌長(三維物體中的一維框架)才能看到物體內部。所以二維小人(如果存在)研究三維立方體只會先把三維立方體的頂點投影在二維平面上,在投影成一條一位的直線。
 正多胞體
正多胞體正如圖片的投影中,立方體的六個面也要把最外部的正方形也要算進去,超正方體表面的八個立方體也包括“最外部”的那一個,可以知道,超正方體有8個胞(立方體)、24個面(正方形)、32條棱和16個頂點。
值得說一下的是,在圖2中,投影后一大一小兩個立方體的邊長比正好是3:1,這個是通過計算得到的。
球極投影
將一個立方體的各個表面膨脹,一段時間後會得到一個球。同樣的方法,將超正方體的表面膨脹,會得到一個“超球”(Hypersphere)。
當我們置身於超正方體膨脹成的超球中的時候,我們就會看見圖片中的這個情景——此時我們置身在“最外部”的立方體(當然是膨脹了的)面上平行投影。
二維線架正投影
四維超正方體不但可以投影到三維,而且也可以直接投影到二維平面上(是直接,不經過三維),但是由於是投影在二維上,會失真得很厲害所以只能夠表現一些點與線之間的連線關係
下圖是超正方體的二維線架正投影,ABCD分別是四個軸,注意“相鄰”兩根軸的夾角都是45度的。16個頂點坐標分別是(±1,±1,±1,±1)(下文有簡單推導),然後按照給出的一個一個填上去就是的了(方法說上去有點煩,大家可以用幾何畫板畫畫這個投影,其實蠻簡單的)。
 正多胞體
正多胞體與十六胞體聯繫
將正八胞體中每個正方體中心作中心所在正方體的正方形面垂線得正十六胞體,正十六胞體作類似處理也可以得正八胞體。
正十六胞體
正十六胞體(Hexadecachoron,16-cell),是一個四維空間裡的幾何產物,正多胞體的其中一種,一般視為正八面體的四維類比。
簡介
它的施萊夫利符號為{3,3,4},是超立方體的對偶。
 正多胞體
正多胞體其頂點圖是正八面體,正16胞體每條棱上有4個正四面體。
另外,它有下列幾種別名:
正四面體反稜柱(Tetrahedron antiprism)、
Tetracross(四維正軸形,沒有官方中文翻譯)、
4-orthoplex(即正四面體反稜柱,orthoplex和cross都指代同一個多胞體,但意義不同)、
Demitesseract(半截超立方體,指代超立方體每個面上連線得到的東東,沒有官方中文翻譯)
施 萊格爾投影
正八面體我們一定不陌生,但是看過右圖的恐怕就不多了。
右圖是當一個人對著正八面體的一個面靠近的很近的時候會看到的——準確地說眼睛是在這個正八面體的外接球面上看到的。這就是正八面體的施萊格爾投影。
可以看到這個投影中外面是一個大正三角形,裡面是一個小的倒正三角形。
 正多胞體
正多胞體運用類比,把正三角形變成正四面體:一個正四面體和一個倒正四面體,再各自連上線,如右下圖,這就得到了一個正十六胞體的施萊格爾投影圖。細心點數的話可以數得出,該圖中有16個四面體(包括最外部的那個),同時我們得到了正十六胞體的一些數據:
胞(正四面體)數:16,面(正三角形)數:32,棱數:24,頂點數:8
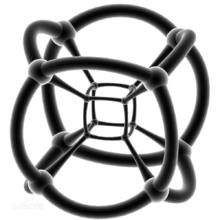
球極投影
將正十六胞體的表面膨脹使之成為一個超球,然後投影到三維上,如圖。
二維線架正投影
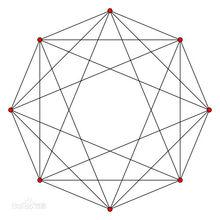 正多胞體
正多胞體和超正方體的差不多,不過要簡單得多,建立一個平面上的四維投影坐標軸,寫入八個點:(±1,0,0,0)(0,±1,0,0)(0,0,±1,0)(0,0,0,±1)即可,如圖所示。
與正八胞體聯繫
將正十六胞體中每個正四面體中心作中心所在正四面體的正三角形面垂線得正八胞體,正八胞體作類似處理也可以得正十六胞體。
正二十四胞體
正二十四胞體(Icositetrachoron,24-cell),有時又作復正八面體(Octaplex=Octahedral complex),表面由24個正八面體構成,是一個四維空間裡的幾何產物,正多胞體中最特殊的一種,因為它沒有三維類比。
簡介
 正多胞體
正多胞體它的施萊夫利符號為{3,4,3},自身對偶
其頂點圖是立方體,正24胞體每條棱上有3個正八面體。
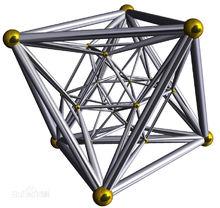
施萊格爾投影
嚴格來說正二十四胞體是沒有三維類比的,因此也不好說是根據哪個正多面體的施萊格爾投影類比到三維上來的。
不過只要根據正二十四胞體每條棱上有3個正八面體這個條件在三維空間上畫投影就不會太難,如右圖。
正二十四胞體的構成數據如下:
胞(正八面體)數:24,面(正三角形)數:96,棱數:96,頂
點數:24
球極投影
 正多胞體
正多胞體將正二十四胞體的表面膨脹使之成為一個超球,然後投影到三維上,如圖。
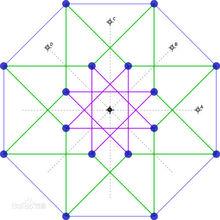
二維線架正投影
如下圖,有線段重合,不太清楚是如何選定坐標的。
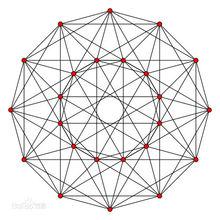 正多胞體
正多胞體聯繫
無聯繫與類比
正一百二十胞體
簡介
正一百二十胞體( hecatonicosachoron, 120-cell),由120個正十二面體胞、720個正五邊形面、1200條棱、600個頂點組成,是四維凸正多胞體,正十二面體的四維類比。
 正多胞體
正多胞體它的施萊夫利符號為{5,3,3},與正六百胞體對偶。
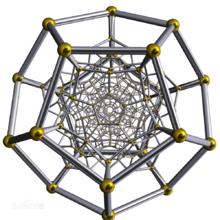
施萊格爾投影
一個有120個正十二面體的多胞體自然不會像正五胞體那樣簡單,如圖
球極投影
將正一百二十胞體的表面膨脹使之成為一個超球,然後投影到三維上,如圖。
 正多胞體
正多胞體二維線架正投影
需要說的是,圖里橙色的點都是有兩個點重疊的。
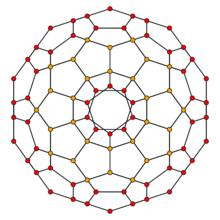 正多胞體
正多胞體與正六百胞體聯繫
將正一百二十胞體中每個正十二面體中心作中心所在正十二面體的正五邊形面垂線得正六百胞體,正六百胞體作類似處理也可以得正一百二十胞體。
正六百胞體
簡介
正六百胞體( hexacosichoron, 600-cell),由600個正四面體胞、1200個正三角形面、720條棱、120個頂點組成,是四維凸正多胞體,正二十面體的四維類比。
它的施萊夫利符號為{3,3,5},與正一百二十胞體對偶。
施萊格爾投影
 正多胞體
正多胞體與正一百二十胞體一樣,正六百胞體的投影也極其複雜,實際上,這是正對著一個頂點投影出來的。(沒錯,就是最中央的那個點)
球極投影
將正六百胞體的表面膨脹使之成為一個超球,然後投影到三維上,如圖。
 正多胞體
正多胞體二維線架正投影
需要說的是,圖里橙色的點都是有兩個點重疊的,黃色的那個點有四個點重疊。
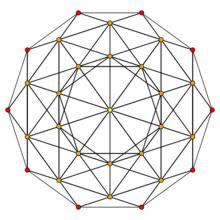 正多胞體
正多胞體與正一百二十胞體聯繫
將正六百胞體中每個正四面體中心作中心所在正四面體的正三角形面垂線得正一百二十胞體,正一百二十胞體作類似處理也可以得正六百胞體。
向更高維類比——正單形(Simplex)編輯
點、線段、正三角形、正四面體、正五胞體……用這種方法一直類比下去 ,得到的所有東西集合在一起,就是正單形。
單形的介紹
單形(Simplex),英文又作Simplexes或Simplices,看上去是Simple和Complex的混合,字面意思大概是簡單的複雜(Simplicial Complex,*.*),說白點就是複雜空間(高維空間)的簡單的東東——可以說,一個單形的確是該空間中構造最簡單的東西。
正單形的定義
在一個n維空間中找到n+1個點,使這些點滿足每兩個點距離相等,那么利用這些點就可以得到一個n維正單形(n-simplex)
通俗地說,正三角形就是二維正單形,正四面體就是三維正單形,正五胞體就是四維正單形。
需要說一下,這個“單形”可不是百度百科上的“晶體單形”,很多網站和網友(包括視頻“教你認識四維空間”)所說的單形指的是四維的單形——五胞體,這裡需要指正一下。單形應該是一個集合。

