機構精確度
正文
機械原理的組成部分,著重研究尺寸和形狀絕對精確的理想機構與實際機構之間的運動誤差。光學儀器、機器人、測量裝置、計算裝置和遠距離控制裝置等精密機械和儀器對機構精確度的要求很高。20世紀30年代以來,對零件製造誤差大小和分布規律的研究引起了人們對研究機構精確度的興趣。1946年,蘇聯人Н.Γ.勃魯也維奇發表了《機構精確度》的著作。但關於空間連桿機構精確度的問題,直到60年代才開始研究。由於零件、構件的尺寸和形狀不可能絕對準確,運動副中也總存在間隙,並受到裝配誤差、工作時的變形和磨損等影響,機構不可避免地會出現運動誤差。零件、構件的製造和裝配誤差,以及由於溫度和受力變形等引起的與名義值的偏差稱為原始誤差。由於實際機構從動件的位置、位移、速度和加速度偏離理想機構相應運動參數所引起的機構的位置、位移、速度和加速度誤差,統稱為機械誤差。誤差越小,精度越高。研究機構精確度的問題,也就是研究機械誤差的問題。機械誤差中主要研究的是機構的位置誤差。
機構位置誤差的分析 當實際機構與理想機構的主動件處在相同位置時,兩機構從動件位置的差別稱為機構的位置誤差,其值Δ嗘 可由泰勒級數展開得到,由於原始誤差Δ
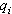 的數值很小,一般只取到線性項
的數值很小,一般只取到線性項 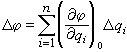 (1)
(1)
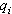 為機構的結構尺寸參數;(
為機構的結構尺寸參數;( 嗘/
嗘/
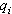 )0為機構在預定位置0時由Δ
)0為機構在預定位置0時由Δ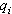 單獨作用而引起從動件運動時的偏傳動比。因此,機構的位置誤差是各原始誤差獨立作用的疊加,稱為位置誤差獨立作用原理。套用這一原理可以簡化機構位置誤差的分析和機構精確度的綜合。
單獨作用而引起從動件運動時的偏傳動比。因此,機構的位置誤差是各原始誤差獨立作用的疊加,稱為位置誤差獨立作用原理。套用這一原理可以簡化機構位置誤差的分析和機構精確度的綜合。 對於成批製造的機構,原始誤差是處於公差範圍內的隨機變數,由它所引起的機械誤差也是隨機變數,稱隨機誤差。隨機誤差的關係式需要套用機率統計理論結合式(1)求得。原始誤差為常態分配時,機械誤差也是常態分配,其平均值μ
 或數學期望E
或數學期望E 以及均方差σ
以及均方差σ 或方差D
或方差D 為
為 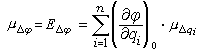
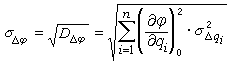 (2)
(2)
 和σ
和σ 分別為原始誤差的平均值和均方差,且μ
分別為原始誤差的平均值和均方差,且μ =(上偏差+下偏差)/2,σ
=(上偏差+下偏差)/2,σ =極限偏差/3。在一般情況下,原始誤差並不全是常態分配。但因每個獨立的原始誤差對機構位置誤差的總和所引起的作用都不顯著,且有足夠的原始誤差個數,所以根據中心極限定理,其總和逼近常態分配,式(2)仍可套用。
=極限偏差/3。在一般情況下,原始誤差並不全是常態分配。但因每個獨立的原始誤差對機構位置誤差的總和所引起的作用都不顯著,且有足夠的原始誤差個數,所以根據中心極限定理,其總和逼近常態分配,式(2)仍可套用。 在誤差分析中,運動副中間隙的影響占有重要的位置。間隙的大小和方向,不但取決於加工質量和潤滑狀態,還與機構的受力情況有關。誤差分析方法有圖解法和解析法。圖解法主要用於平面機構,其中有轉化機構微小位移法和作用線增量法。對典型的簡單空間機構則採用解析法,其中有增加坐標系法(每個件上引進兩個坐標系)和將間隙向量折算為有關結構參數附加誤差量的方法等,常以矩陣形式用電子計算機求解,式(1)為基本機構的位置誤差分析式。對於由多個基本機構組成的各種組合機構,其誤差分析類似公式(1)的基本原則,根據不同的運動傳遞方式導出各種關係式。
機構精確度的綜合 按給定精度要求制定零件、構件的公差和運動副中的間隙,是機構位置誤差分析的逆過程。通常先從誤差分析中找出機械誤差最大的位置,然後按此位置進行綜合。設計時先分析原始誤差對機械誤差的影響。對於影響較大的一些原始誤差,按其大小和正負定出它們之間的公差比值,再進行設計,定出精度等級。餘下的精度等級可按同一級或低一級的精度選取。對於精度要求較高的機構可採用多目標函式的最佳化設計,如在要求機構的運動誤差最小和成本最低的前提下,同時又要滿足機構給定的精度要求,則應定出所需的各設計參數。
對於用幾個基本機構串聯而成的機構或組合機構,在精確度設計時首先應使機構造型合理:尺寸鏈要短,在機構工作區間的各偏傳動比和壓力角要小。另外,在誤差分析中,應把關鍵機構作為重點考慮,如精密減速器中的低速級。最後一級的精度要求尤高。為保證這對齒輪無側隙的嚙合傳動,常將其中一個製成雙片齒輪,用彈簧拉緊,使輪齒錯位以消除空程,這種消除或減少誤差影響的裝置稱為誤差補償裝置。誤差補償方法很多,如套用可調節的凸輪曲面產生的附加運動來消除或減少機械誤差。
隨著人造衛星和機器人等迅速發展,空間機構的精確度越來越引起人們的重視。關於這方面的研究,在雙萬向聯軸節和空間四桿機構中已取得很大的成果,而對於包括五桿以上的連桿機構、凸輪機構等一般空間機構,尚待建立普遍適用的誤差分析方法,並考慮各種工況的多目標最佳化綜合,進而考慮動力誤差的綜合。