黑體
[中文]: 黑體輻射
黑體輻射[英文]: black-body radiation
黑體輻射源
什麼是黑體？
在任何條件下，對任何波長的外來輻射完全吸收而無任何反射的物體，即吸收比為1的物體。
在黑體輻射中，隨著溫度不同，光的顏色各不相同，黑體呈現由紅——橙紅——黃——黃白——白——藍白的漸變過程。某個光源所發射的光的顏色，看起來與黑體在某一個溫度下所發射的光顏色相同時，黑體的這個溫度稱為該光源的色溫。“黑體”的溫度越高，光譜中藍色的成份則越多，而紅色的成份則越少。例如，白熾燈的光色是暖白色，其色溫表示為2700K，而日光色螢光燈的色溫表示則是6000K。
定義
黑體受熱以電磁波的形式向外輻射能量，是一種理想物體的熱輻射。
所謂黑體是指能夠全部吸收入射的任何頻率的電磁波的理想物體，實際上黑體是不存在的。但可以用某種裝置近似地代替黑體。一個帶有小孔的空腔，並且小孔對於空腔足夠小，不會妨礙空腔內的平衡。通過小孔射入空腔的所有頻率的電磁波經腔內壁多次反射後，幾乎全部被吸收，再從小孔射出的電磁波極少。所以，可以將空腔上的小孔近似地看成黑體。
在溫度T下,空腔壁也跟其他固體一樣，不斷輻射電磁波，腔內形成一輻射場，經過一定時間，腔內的輻射場與腔壁達到了熱平衡。這時平衡輻射的性質只依賴於溫度，與腔壁的其他性質無關。由於小孔是腔上的一部分，也處於同樣的溫度，因此，小孔的輻射性質就代表了空腔內的輻射性質。
可以證明，黑體單位表面積單位時間發出的總輻射能量,即輻射通量密度（又稱輻射出射度）M,與輻射場總能量密度ω之間的關係
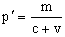黑體輻射式中с為光速，ω(T)只依賴於溫度。
在統計物理學中，把空腔內的輻射場看作光子氣體，光子是玻色子，根據玻色分布可以導出處於平衡的黑體輻射場能量密度按頻率的分布即普朗克公式。也可求得描述黑體輻射場的總能量與熱力學溫度間關係的斯忒藩－玻耳茲曼定律，和黑體輻射的物態方程
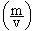黑體輻射式中p 是輻射壓力。上述由統計物理得到的關於黑體輻射的公式和定律與實驗結果完全符合。
理論數據
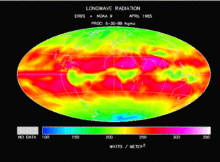地球黑體輻射普朗克輻射定律(Planck)則給出了黑體輻射的具體譜分布，在一定溫度下，單位面積的黑體在單位時間、單位立體角內和單位波長間隔內輻射出的能量為：
B(λ，T)=2hc2 /λ5 /exp(hc/λKT)-1
B(λ，T)—黑體的光譜輻射亮度(W·m^-2·Sr^-1·μm^-1 )
黑體光譜輻射出射度M（λ，T）與波長、熱力學溫度之間關係的公式：
M=c1/[λ^5(exp(c2/λT)-1)]，其中c1=2πhc^2,c2=hc/k.
黑體能量密度公式：
E*dν=c1*v^3*dv/[exp(c2*v/T)-1)]
E*dv表示在頻率範圍（v,v+dv）中的黑體輻射能量密度。
λ—輻射波長(μm)
T—黑體絕對溫度(K、T=t+273k)
C—光速(2.998×10^8m/s )
h—普朗克常數， 6.626×10^-34 J/S
K—玻爾茲曼常數(Boltzmann)， 1.3806505*10^-23J/K基本物理常數
由圖2.2（缺）可以看出：
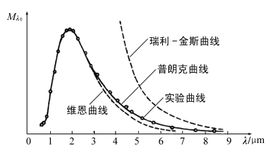
①在一定溫度下，黑體的譜輻射亮度存在一個極值，這個極值的位置與溫度有關， 這就是維恩位移定律(Wien)
λm T=2.898×10(μm·K)
λm —最大黑體譜輻射亮度處的波長(μm)
T—黑體的絕對溫度(K)
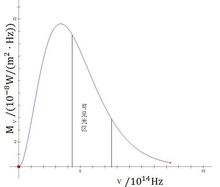太陽輻射波譜密度分布根據維恩定律，我們可以估算，當T～6000K時，λm ～0.48μm(綠色)。這就是太陽輻射中大致的最大譜輻射亮度處。
當T～300K， λm～9.6μm，這就是地球物體輻射中大致最大譜輻射亮度處。
②在任一波長處,高溫黑體的譜輻射亮度絕對大於低溫黑體的譜輻射亮度，不論這個波長是否是光譜最大輻射亮度處。
如果把B(λ，T)對所有的波長積分，同時也對各個輻射方向積分，那么可得到斯特番—波耳茲曼定律(Stefan-Boltzmann)，絕對溫度為T的黑體單位面積在單位時間內向空間各方向輻射出的總能量為B(T)
B(T)= δT4 (W/m2)
δ為Stefan-Boltzmann常數, 等於5.67×10ˆ-8 W/m2·K4
但現實世界不存在這種理想的黑體，那么用什麼來刻畫這種差異呢?對任一波長， 定義發射率為該波長的一個微小波長間隔內， 真實物體的輻射能量與同溫下的黑體的輻射能量之比。顯然發射率為介於0與1之間的正數，一般發射率依賴於物質特性、 環境因素及觀測條件。如果發射率與波長無關，那么可把物體叫作灰體(grey body)， 否則叫選擇性輻射體。
