簡介
模形式論是更廣泛的自守形式理論的特例。自守形式理論的發展大致可分成三期:
19世紀初:探討與橢圓函式相關的方面。
19世紀末:此時單變數自守形式的概念誕生。此理論由菲利克斯·克萊因等人發展。
1925至1960年:由赫克發端,發現了模形式與數論的聯繫。
1.19世紀初:探討與橢圓函式相關的方面。
2.19世紀末:此時單變數自守形式的概念誕生。此理論由菲利克斯·克萊因等人發展。
3.1925至1960年:由赫克發端,發現了模形式與數論的聯繫。
作為格的函式
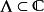 模形式論
模形式論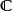 模形式論
模形式論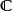 模形式論
模形式論 模形式論
模形式論一個模形式可視為從所有格 (即: 中的離散加法子群,使得其商群緊緻)的集合映至 的函式 ,使之滿足下述條件 :
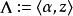 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論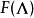 模形式論
模形式論 模形式論
模形式論1) 若考慮形如 之格,其中 為常數而 為變數,則 是 的全純函式。
 模形式論
模形式論 模形式論
模形式論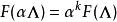 模形式論
模形式論2) 存在常數 (通常取正整數),使得對任何 ,有 。常數k稱為此模形式之 權。
 模形式論
模形式論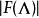 模形式論
模形式論3) 對於最小非零元與原點距離大於一定值之格 , 有上界。
 模形式論
模形式論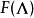 模形式論
模形式論 模形式論
模形式論當 ,條件二表明 僅決定於 在相似變換下的等價類。這是重要的特例,但是權為零的模形式必為常數函式。若去掉條件三,並容許函式有極點,則存在非常數的例子,稱作 模函式。
 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論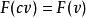 模形式論
模形式論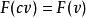 模形式論
模形式論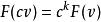 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論這個狀況可以與射影空間 作類比:對於射影空間,我們欲尋找向量空間 上對座標的多項式函式 ,並滿足 ;不幸的是,這種函式必為常數。一種辦法是容許有分母(即考慮有理函式),則滿足條件的是分子、分母為同次數齊次多項式的有理函式。另一種辦法則是修改條件 為 ,則滿足此條件的函式為 次齊次多項式,對每個固定的 ,這些函式構成有限維向量空間。借著考慮所有可能的 ,我們可以找出構造 上的有理函式所需之分子與分母。
 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論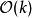 模形式論
模形式論 模形式論
模形式論既然 次齊次多項式在 上並非真正的函式,該如何從幾何上詮釋?代數幾何給出了一個答案:它們是 上某個層 的截面。模形式的情形也類似,但考慮的不是 ,而是某個模空間。
作為橢圓曲線模空間上的函式
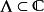 模形式論
模形式論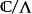 模形式論
模形式論每個格 都決定一條復橢圓曲線 ;兩個格給出的橢圓曲線同構的充要條件是兩個格之間差一個非零複數的倍數。因此模函式可以看作是復橢圓曲線的模空間上的函式。例如橢圓曲線的j-不變數就是模函式。模形式可視作模空間上某些線叢的截面。
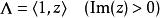 模形式論
模形式論 模形式論
模形式論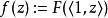 模形式論
模形式論 模形式論
模形式論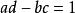 模形式論
模形式論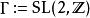 模形式論
模形式論每個格在乘上某個非零複數倍數後皆可表成 。對一模形式 ,置 。模形式的第二個條件可改寫成函式方程:對所有 且 (即模群 之定義),有
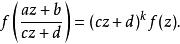 模形式論
模形式論 模形式論
模形式論例如,取 :
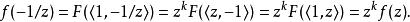 模形式論
模形式論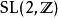 模形式論
模形式論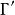 模形式論
模形式論 模形式論
模形式論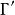 模形式論
模形式論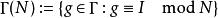 模形式論
模形式論如果上述方程僅對 內的某個有限指數子群 成立,則稱 為對 的模形式。最常見的例子是同餘子群 ,以下將詳述。
廣義定義
 模形式論
模形式論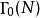 模形式論
模形式論令 為正整數,相應的模群 定義為:
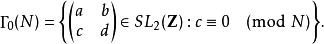 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論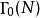 模形式論
模形式論 模形式論
模形式論令 為正整數,權為 的 級(或級群為 )模形式定義為一個上半平面上的全純函式,對任何
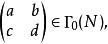 模形式論
模形式論 模形式論
模形式論及任何屬於上半平面的 ,有
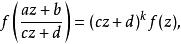 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論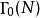 模形式論
模形式論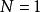 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論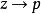 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論而且在尖點全純。所謂 尖點,是在作用下的軌道。例如當時,代表了唯一的尖點。模形式在尖點全純,意謂時有界。當此尖點為時,這等價於有傅立葉展開式
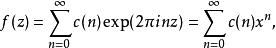 模形式論
模形式論 模形式論
模形式論其中。對於其它尖點,同樣可藉座標變換得到傅立葉展開。
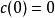 模形式論
模形式論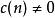 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論若對每個尖點都有,則稱之為尖點形式。使得的最小稱作在該尖點的階。以上定義的模形式有時也稱為整模形式,以區分帶極點的一般情形(如j-不變數) 。
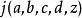 模形式論
模形式論 模形式論
模形式論另一種的推廣是考慮某類函式,並將函式方程改寫為
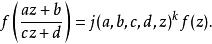 模形式論
模形式論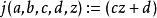 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論 模形式論
模形式論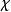 模形式論
模形式論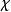 模形式論
模形式論 模形式論
模形式論上式所取的稱為 自守因子。若另取適當的,則在此框架下亦可探討戴德金η函式,這是權等於1/2的模形式。例如:一個權等於、級、 nebentypus為(是模的一個狄利克雷特徵)是定義於上半平面,並具下述性質的全純函式:對任意
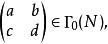 模形式論
模形式論 模形式論
模形式論及屬於上半平面的,有函式方程
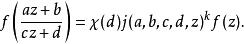 模形式論
模形式論 模形式論
模形式論此外,必須在尖點全純。
其他模函式概念的推廣
模函式的概念還能做一些推廣。
例如,可以去掉全純條件:馬斯形式是上半平面的拉普拉斯運算元的特徵函式,但並非全純函式。
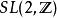 模形式論
模形式論 模形式論
模形式論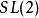 模形式論
模形式論此外,可以考慮以外的群。希爾伯特模形式是個變元的函式,每個變元都屬於上半平面。其函式方程則由分布於某個全實域的二階方陣來定義。若以較大的辛群取代,便得到西格爾模形式。模形式與橢圓曲線相關,而西格爾模形式則涉及更廣義的阿貝爾簇。
自守形式的概念可用於一般的李群。

