模式識別法

簡介

穩定性事故是涉及電力系統全局的重大事故。正常運行中的電力系統是否會因為一個突然發生的事故而導致失去穩定，是電力系統分析的一個主要方面。校核假想事故後電力系統是否能保持穩定運行的離線穩定計算，一般採用數值積分法，逐時段地求解描述電力系統運行狀態的微分方程組，得到動態過程中狀態變數隨時間變化的規律，並用此來判別電力系統的穩定性。這種方法計算工作量很大，無法滿足實施預防性控制的實時性要求。因此要尋找一種快速的穩定性判別方法。但到目前為止，還沒有很成熟的算法，下面簡單介紹一下已取得一定研究成果的模式識別法、李雅普諾夫法以及我國學者創新研發的擴展等面積法。

模式識別法

模式識別法是建立在對電力系統各種運行方式的假想事故離線模擬計算的基礎上的，需要事先對各種不同運行方式和故障種類進行穩定計算，然後選取少數幾個表征電力系統運行的狀態變數(一般是節點電壓和相角)，通過自學過程構成穩定判別式，在做穩定分析時，將線上實測的運行參數代入穩定判別式，根據判別式的結果來判斷系統是否穩定。

模式識別法的原理

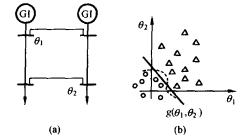圖1簡單電力系統及其特徵量平面圖

圖1是運用模式識別法進行穩定性判定的示意圖。圖中θ和θ是兩個表征電力系統的狀態變數，針對不同的運行方式和假想事故，分別在θ-θ平面上就標出了許多穩定情況(用○點表示)和不穩定情況(用△點表示)。如果○點和△點分布各自集中在某一區域，在它們之間有一條明確的分界線，該分界線的方程就是 穩定判別式，可根據實時計算的θ和θ在θ-θ平面中所處的區域，快速地判別是否穩定。在圖1中分界線如為直線則判別式非常簡單，直線的左側是穩定的，右側是不穩定的。若分界線是為一曲線，則要稍稍複雜一點。實際上，表征電力系統的特徵量是多維的，穩定域和不穩定域之間的分界面(不再是分界線)是一超平面。

模式識別法的優缺點

模式識別法是一個快速的判別電力系統安全性的方法，只要將特徵量代人判別式就可以得出結果。所以這個判別式本身必須可靠。誤差率很大的判別式沒有實用價值。判別式的建立，不是靠理論推導，而是通過大量“樣本”計算後歸納整理出來的。如何使這樣歸納整理出來的判別式儘量逼近客觀存在的分界面，不是一件容易的事。

其他算法簡介

1.李雅普諾夫方法

李雅普諾夫法是在狀態空間中找出一個包含穩定平衡點的區域，使得凡是屬於這一區域的任何擾動，系統以後的運動最終都趨於穩定平衡點。這一區域稱為關於穩定平衡點的漸近穩定域，簡稱穩定域。為了求得穩定域，需要構造李雅普諾夫函式，或稱V函式。通過V函式和系統狀態方程，就可以決定穩定域。在進行電力系統動態過程計算時，不必計算出整個動態過程隨時間變化的曲線，而只要計算出系統最後一次操作時的狀態變數(即故障切除後的狀態變數)，並相應計算出該時刻的V函式值。將該函式值與最鄰近的不穩定平衡點的V函式值進行比較，如果前者小於後者，系統就是穩定的。反之系統是不穩定的。這個方法避免了常規穩定計算時大量的數值積分計算，計算速度比較快，是一種有前途的適用於實時控制的計算方法。但是如何建立適合於複雜系統的李雅普諾夫函式和如何計算最鄰近的不穩定平衡點都還沒有很好解決。計算結果也偏於保守，所以該方法還尚未在電力系統中得到實際套用。

2.擴展等面積法EEAC

擴展等面積法EEAC是我國學者首創的一種暫態穩定快速定量計算方法，已成功開發出世界上至今唯一的暫態定量分析商品軟體，並已套用於國內外電力系統的各項工程實踐中。