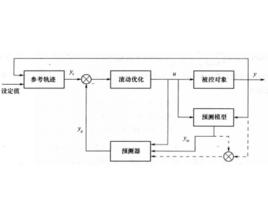
發展背景
20世紀60年代初期發展起來並日趨完善的現代控制理論,具有最優的性能指標和系統而精確的理論設計方法,在航天航空、制導等領域中獲得了卓越的成就。但是在套用於工業過程控制時卻沒有收到預期的效果。究其原因,現代控制理論的基礎是精確的對象參數模型,而工業過程往往具有非線性、時變性、強耦合和不確定性等特點,難以得到精確的數學模型,因而控制效果將大大降低。面對理論發展與實際套用之間的不協調,人們從工業過程控制的特點與需求出發,探索各種對模型精度要求不高而同樣能實現高質量控制的方法。模型預測控制(Model Predictive Control,簡稱預測控制)正是在這種背景下應運而生的一類新型控制算法。一經問世,它就在石油、電力和航空等工業中得到十分成功的套用並迅速發展起來。因此,預測控制的出現並不是某種理論研究的產物,而是在工業實踐過程中發展起來的一種有效的控制方法。
基本組成
(1)預測模型
預測控制應具有預測功能,即能夠根據系統的現時刻的控制輸入以及過程的歷史信息,預測過程輸出的未來值,因此,需要一個描述系統動態行為的模型作為預測模型。
在預測控制中的各種不同算法,採用不同類型的預測模型,如最基本的模型算法控制(MAC)採用的是系統的單位脈衝回響曲線,而動態矩陣控制(DMC)採用的是系統的階躍回響曲線。這兩者模型互相之間可以轉換,且都屬於非參數模型,在實際的工業過程中比較容易通過實驗測得,不必進行複雜的數據處理,儘管精度不是很高,但數據冗餘量大,使其抗干擾能力較強。
預測模型具有展示過程未來動態行為的功能,這樣就可像在系統仿真時那樣,任意的給出未來控制策略,觀察過程不同控制策略下的輸出變化,從而為比較這些控制策略的優劣提供了基礎。
(2)反饋校正
在預測控制中,採用預測模型進行過程輸出值的預估只是一種理想的方式,在實際過程中。由於存在非線性、模型失配和干擾等不確定因素,使基於模型的預測不可能準確地與實際相符。因此,在預測控制中,通過輸出的測量值Y(k)與模型的預估值Ym(k)進行比較,得出模型的預測誤差,再利用模型預測誤差來對模型的預測值進行修正。
由於對模型施加了反饋校正的過程,使預測控制具有很強的抗擾動和克服系統不確定性的能力。預測控制中不僅基於模型,而且利用了反饋信息,因此預測控制是一種閉環最佳化控制算法。
(3)滾動最佳化
預測控制是一種最佳化控制算法,需要通過某一性能指標的最最佳化來確定未來的控制作用。這一性能指標還涉及到過程未來的行為,它是根據預測模型由未來的控制策略決定的。
但預測控制中的最佳化與通常的離散最優控制算法不同,它不是採用一個不變的全局最優目標,而是採用滾動式的有限時域最佳化策略。即最佳化過程不是一次離線完成的,而是反覆線上進行的。在每一採樣時刻,最佳化性能指標只涉及從該時刻起到未來有限的時間,而到下一個採樣時刻,這一最佳化時段會同時向前。所以,預測控制不是用一個對全局相同的最佳化性能指標,而是在每一個時刻有一個相對於該時刻的局部最佳化性能指標。
(4)參考軌跡
在預測控制中。考慮到過程的動態特性,為了使過程避免出現輸入和輸出的急劇變化,往往要求過程輸出y(k)沿著一條期望的、平緩的曲線達到設定值r。這條曲線通常稱為參考軌跡y,。它是設定值經過線上“柔化”後的產物。
基本算法
目前,預測控制的算法有幾十種,其中具有代表性的主要有模型算法控制(MAC)、動態矩陣控制(DMC)和廣義預測控制(GPC)等。
(1)模型算法控制
模型算法控制的原理結構圖與圖8—7相似。模型算法控制的結構包括四個計算環節.即內部模型、反饋校正、滾動最佳化及參考軌跡。
這種算法的基本思想為:首先預測對象未來的輸m狀態.再以此來確定當前時刻的控制動作,即先預測再控制。由於它具有一定的預測性,使得它明顯優於傳統的先輸出後反饋冉控制的PID控制系統。
模型算法控制的具體算法很多,有單步模型算法控制、多步模型算法控制、單值模型算法控制和增量型模型算法控制等,這裡不再詳述。
(2)動態矩陣控制
動態矩陣控制與模型算法控制的不同之處在於內部模型上。該算法採用的是工程上易於測取的對象階躍回響做模型。其算法較簡單,計算量少且魯棒性強,在石化工業中得到了廣泛的套用。
(3)廣義預測控制
廣義預測控制是在前面幾種預測算法的基礎上,引入了自適應控制的思想。一般的預測控制算法主要通過反饋來補償系統誤差,再加上滾動最佳化技術,使模型能對因時變、干擾等造成的影響及時進行補償。但這種說法是相對的,如果內部模型的準確性很差.則仍會對系統的穩定性造成嚴重的影響。廣義預測控制就是面向此類問題的解決方案。
優點
從預測控制的基本原理來看,這類方法具有下列明顯的優點:
(1)建模方便。過程的描述可以通過簡單的實驗獲得。不需要深入了解過程的|人J部機理。
(2)採用了非最小化描述的離散卷積和模型,信息冗餘量大,有利於提高系統的魯棒性。
(3)採用了滾動最佳化策略,即線上反覆進行最佳化計算,滾動實施,使模型失配、畸變、擾動等引起的不確定性及時得到彌補,從而得到較好的動態控制性能。
特點
與其他控制算法相比,預測控制有其自身的特點:
(1)對模型的精度要求不高,建模方便,過程描述可由簡單實驗獲得;
(2)採用非最小化描述的模型,系統魯棒性、穩定性較好;
(3)採用滾動最佳化策略,而非全局一次最佳化,能及時彌補由於模型失配、畸變、干擾等因素引起的不確定性,動態性能較好;
(4)易將算法推廣到有約束、大遲延、非最小相位、非線性等實際過程,尤為重要的是,它能有效地處理多變數、有約束的問題。
套用前景
預測控制理論雖然在上個世紀70年代就已提出,在工程實踐中也有成功套用的案例,但是經過了近四十年的發展,還有很多問題值得更深入的探索和研究。
1)預測控制理論研究。預測控制的起源與發展與工程實踐緊密相連。實際上理論研究遲後於實踐的套用。主要設計參數與動靜態特性,穩定性和魯棒性的解析關係很難得到。且遠沒達到定量的水平。
2)對非線性,時變的不確定性系統的模型預測控制的問題還沒有很好的解決。
3)將滿意的概念引入到系統設計中來,但滿意最佳化策略的研究還有待深入。
4)預測控制算法還可以繼續創新。將其他學科的算法或理論與預測控制算法相結合,如引入神經網路、人工智慧、模糊控制等理論以更加靈活的適應生產需要。
從模型預測控制理論和實踐的飛速發展來看,預測控制已經存在大量成功的工業套用案例,一些線性預測和非線性預測工程軟體包已經推出和套用。傳統預測控制理論研究日臻成熟,預測控制與其他先進控制策略的結合也強益緊密。預測控制已成為一種極具工業套用前景的控制策略。