簡介
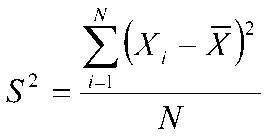 標準偏差
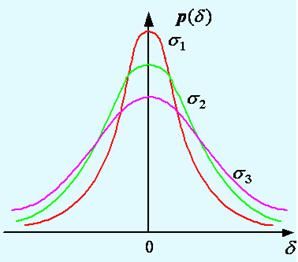
標準偏差一種量度數據分布的分散程度之標準,用以衡量數據值偏離算術平均值的程度。標準偏差越小,這些值偏離平均值就越少,反之亦然。標準偏差的大小可通過標準偏差與平均值的倍率關係來衡量。
在重複測量給出不同結果時,需要了解這些讀數分散範圍有多寬。測量結果的分散範圍告訴了我們關於測量不確定度的情況。通過了解讀數分散範圍有多大,就能著手判斷這次測量或這組測量的質量如何。
定量給出分散範圍的常見形式是標準偏差。一個數集的標準偏差給出了各個讀數與該組讀數平均值之差的典型值。
根據“經驗”,全部讀數大概有三分之二(68.27%)會落在平均值的正負(±)1倍標準偏差範圍內,大概有全部讀數的95%會落在正負2倍標準偏差範圍內。雖然這種“尺度”並非普遍適用,但套用廣泛。標準偏差的“真值”只能從一組非常大(無窮多)的讀數求出。由有限個數的讀數所求得的只是標準偏差的估計值,稱為實驗標準偏差或估計的標準偏差,用符號s表示。
套用
標準偏差是一種表示分散程度的統計觀念。標準偏差已廣泛運用在股票以及共同基金投資風險的衡量上,主要是根據基金淨值於一段時間內波動的情況計算而來的。一般而言,標準偏差愈大,表示淨值的漲跌較劇烈,風險程度也較大。實務的運作上,可進一步運用單位風險報酬率的概念,同時將報酬率的風險因素考慮在內。所謂單位風險報酬率是指衡量投資人每承擔一單位的風險,所能得到的報酬,以夏普指數最常為投資人運用。標準偏差是一組數值自平均值分散開來的程度的一種測量觀念。一個較大的標準偏差,代表大部分的數值和其平均值之間差異較大;一個較小的標準偏差,代表這些數值較接近平均值。
公式
 標準偏差
標準偏差計算
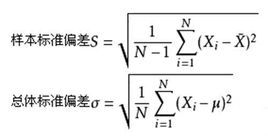
樣本標準偏差的計算步驟是:步驟一、(每個樣本數據減去樣本全部數據的平均值)。
步驟二、把步驟一所得的各個數值的平方相加。
步驟三、把步驟二的結果除以(n-1)(“n”指樣本數目)。
步驟四、從步驟三所得的數值之平方根就是抽樣的標準偏差。
總體標準偏差的計算步驟是:
步驟一、(每個樣本數據減去總體全部數據的平均值)。
步驟二、把步驟一所得的各個數值的平方相加。
步驟三、把步驟二的結果除以n(“n”指總體數目)。
步驟四、從步驟三所得的數值之平方根就是總體的標準偏差。
舉例
有一組數字分別是200、50、100、200,求它們的標準偏差。x撥 = (200+50+100+200)/4 = 550/4 = 137.5
S^2 = ((200-137.5)^2+(50-137.5)^2+(100-137.5)^2+(200-137.5)^2)/(4-1) = (62.5^2+(-87.5)^2+(-37.5)^2+62.5^2)/3 = (3906.25+7656.25+1406.25+3906.25)/3 = 16875/3 = 5625
標準偏差 S = Sqr(5625) = 75