定義
在黎曼流形中平均曲率向量(即它的第二基本型的跡) 為零的子流形稱為極小子流形。二維的極小子流形稱為極小曲面。一維極小子流形就是測地線。
歐幾里得空間中子流形是極小的,若且唯若其坐標函式是該子流形上的調和函式。具有非正截面曲率的完備單連通黎曼流形中不存在閉的極小子流形。
幾何意義
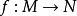 極小子流形
極小子流形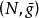 極小子流形
極小子流形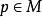 極小子流形
極小子流形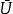 極小子流形
極小子流形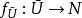 極小子流形
極小子流形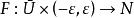 極小子流形
極小子流形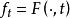 極小子流形
極小子流形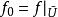 極小子流形
極小子流形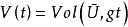 極小子流形
極小子流形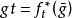 極小子流形
極小子流形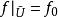 極小子流形
極小子流形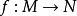 極小子流形
極小子流形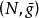 極小子流形
極小子流形極小子流形的幾何意義是: 設 是浸入在黎曼流形 中的子流形。如果每一點 都有一個開鄰域 U,使得 是緊緻的,並且對於 的任意一個有固定邊界的變分 (記 ,且 ),體積泛函 (其中 )都以 為其臨界點,則 是浸入在黎曼流形 中的極小子流形。反之亦然。
發展
極小曲面的高維推廣是由李普希茨開始的,他給出了梅斯尼埃關於極小曲面幾何解釋的推廣,並且證明了黎曼流形中的子流形是其體積泛函的臨界點若且唯若其平均曲率向量為0。
在其後很長一段時期里,極小子流形的發展基本上限於局部性質的研究。
在近代,極小子流形的研究主要是整體性質以及局部性質與整體性質的關係,其發展非常迅速,出現了很多驚人的重要結果和不少有趣的新問題,尤其是極小超曲面和空間形式的極小子流形理論中更是如此。
另外,極小曲面理論在三維拓撲學中的套用也獲得了意外的成功。極小子流形現在已構成微分幾何學的一個極其重要的分支,它與微分幾何學的其他分支以及微分方程、拓撲學、幾何測度論、複變函數等都有密切聯繫,並在物理學中有重要套用。
關於極小子流形的整體性研究,陳省身、項武義、丘成桐等都做出了重要貢獻。

