定義
格點分布
格點分布
格點分布
格點分布
格點分布定義一：格點分布(lattice distribution)亦稱格子點分布，是一種基本的離散型分布。若離散型隨機變數ξ取的值，是直線上的等距點列，其分布列為，則稱ξ服從 格點分布。其中為任意整數，為固定實數，二項分布，泊松分布都是格點分布的特殊情況 。
格點分布
格點分布
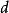格點分布
格點分布定義二： 若存在，使得，則稱隨機變數服從格點分布，滿足上述條件的最大的是此格點分布的周期 。
圓格點分布
格點分布圓格點分布(circular lattice distribution)是一種算術分布。稱隨機變數X有圓格點分布，如果其一切可能值可以表示為，其中α和n為常數。
相關定理
費勒(FelIer)初等更新定理
格點分布
格點分布
格點分布
格點分布記，則，若，則。
布萊克韋爾(Blackwell)更新定理
格點分布記，有：
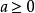格點分布
格點分布
格點分布(1) 若F不是格點的，則對一切，當時有。
格點分布
格點分布
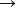格點分布(2) 若F是格點的，周期為d，則當時，有P{在nd處發生更新)。
關鍵更新定理(史密斯(smith)更新定理)
格點分布
格點分布記，設函式，滿足：
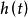格點分布①非負不增；
格點分布
格點分布
格點分布②，設是更新方程的解，有
(1)若F不是格點的，則
格點分布
格點分布(2)若F是格點的，對於，則
格點分布交錯更新過程
格點分布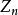
格點分布
格點分布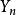
格點分布
格點分布設一個過程有“開”、“關”兩個狀態，先“開”，持續一段時間後又“關”，持續一段時間後又“開”，再持續一段時間後又“關”......如此“開”、“關”下去。設“開”的時間為，“關”的時間為是獨立同分布隨機變數，是獨立同分布隨機序列，但與不相互獨立。則更新過程稱為 交錯更新過程 。
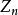格點分布
格點分布
格點分布
格點分布
格點分布
格點分布
格點分布若交錯更新過程中的分布為的分布為的分布函式為，記{過程在時刻為“開”)。則當，且F是非格點分布時，有
格點分布