簡介
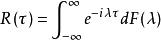 譜分布函式
譜分布函式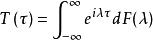 譜分布函式
譜分布函式在連續參數情形,設{X(t),t∈(-∞,∞)}是均方連續的寬平穩過程,R()是它的相關函式。由R(T)的非負定性和波博赫納-辛欽定理知,存在有界非降右連續函式F,使得,這時稱函式 F 為過程的譜分布函式,也有文獻稱過程的協方差函式 () 通過確定的有界非降右連續函式 F 為過程的譜分布函式。
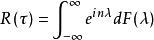 譜分布函式
譜分布函式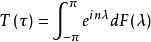 譜分布函式
譜分布函式在離散參數情形,設{X (t),t=0,±1,±2,…}是寬平穩序列,R()是它的相關函式,則存在[-,]上有界非降右連續函式 F ,使得或使得協方差函式,這時稱F為序列的譜分布函式。
譜分布函式 F 不是惟一的,但它們之間最多相差一常數。由相關函式 R() 與由協方差函式 (r) 確定的譜分布函式不同之處是它們對應的勒貝格-斯蒂爾傑斯測度在 0 點相差一常數。
相關函式譜分解
[spectral decomposition of correlation function]
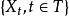 譜分布函式
譜分布函式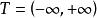 譜分布函式
譜分布函式相關函式譜分解亦稱相關函式譜表示(spectral representation of correlation function)或譜展式(spectral expansion equation)。將相關函式表示為其譜分布函式的傅立葉變式。設弱平穩過程 有相關函式 R(t),則當 時有
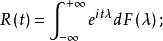 譜分布函式
譜分布函式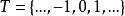 譜分布函式
譜分布函式而當 時有
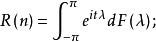 譜分布函式
譜分布函式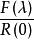 譜分布函式
譜分布函式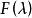 譜分布函式
譜分布函式 譜分布函式
譜分布函式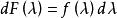 譜分布函式
譜分布函式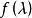 譜分布函式
譜分布函式此即相關函式的譜分解式,其中 是機率分布函式,稱 為 的 譜分布函式。特別地,當 ,稱此 為譜密度函式(spectral density function)。相關函式的模可積是譜密度存在的一個充分條件。
自協方差的譜表示
[spectral representation of autocovariance]
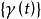 譜分布函式
譜分布函式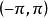 譜分布函式
譜分布函式記平穩序列的自協方差函式為 ,根據譜表示理論,自協方差有如下的譜表示,即存在 上的非降的函式 F(x) 使得
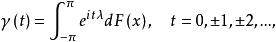 譜分布函式
譜分布函式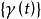 譜分布函式
譜分布函式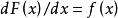 譜分布函式
譜分布函式稱 F(x) 為自協方差 的 譜分布函式。當F(x) 有密度函式時,即 時,則有
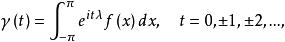 譜分布函式
譜分布函式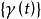 譜分布函式
譜分布函式稱 f(x) 為 的譜分布密度函式(spectral density function)。
根據譜理論,自協方差函式與譜分布是相互唯一確定的,所以它們所描述序列的特性,本質上是相同的。在實際套用中,主要是根據序列的樣本數據 x(1),x(2),...,x(T),對譜分布的統計理論與方法有較長的歷史,擁有較完備和豐富的文獻資料,多年來已在諸多領域中被實際套用。

