推導
朗道量子化可以通過準經典的方法部分導出。這裡採用量子力學的方法進行推導:
考慮一個帶電粒子組成的二維系統。這些粒子無內部相互作用,所帶電荷為q,自旋量子數為S,並被限制在x-y平面內一個面積A=LL的區域內。
 朗道規範
朗道規範對這一系統施加一個沿z軸的均勻磁場 。由於自旋對於這個二維系統沒有影響,因而在下面的推導中將忽略自旋。在CGS單位制下,這個系統的哈密頓算符為:
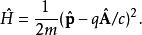 朗道規範
朗道規範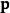 朗道規範
朗道規範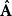 朗道規範
朗道規範式中 為正則動量算符, 為磁場的磁矢勢,與磁感應強度的關係為:
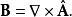 朗道規範
朗道規範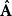 朗道規範
朗道規範給定磁場的磁矢勢具有一定的規範自由度。當 被添加一個標量場的梯度時,波函式的整體相位也會隨著標量場產生一定的變化,但由於哈密頓算符具有規範不變性,系統的物理性質並不受選定的規範影響。為了簡便計算,這裡選擇朗道規範:
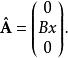 朗道規範
朗道規範式中B=| B|, x為位置算符x方向上的分量。
在這一規範下,系統的哈密頓算符為:
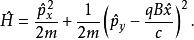 朗道規範
朗道規範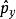 朗道規範
朗道規範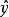 朗道規範
朗道規範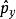 朗道規範
朗道規範算符 與這一哈密頓算符是對易的。這是因為在選定規範時,算符 被忽略掉了,因而算符 可被它的本徵值 ħk替代。
如果設定迴旋頻率ω= qB/mc,那么可以得出此時哈密頓算符為:
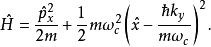 朗道規範
朗道規範這與量子諧振子的哈密頓算符基本一致,但勢能的最小值需要在位置表象中移動 x= ħk/mω。
為了得出能量,我們假設對於諧振子勢能的平移並不會影響到系統的能量,也就是說這一系統的能量與標準的量子諧振子一致:
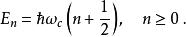 朗道規範
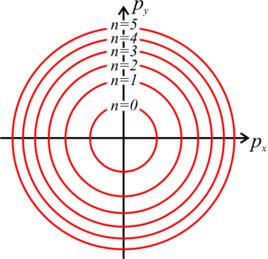
朗道規範由於能量與量子數 k無關,因而會存在一定的簡併態。
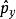 朗道規範
朗道規範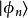 朗道規範
朗道規範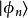 朗道規範
朗道規範由於 與哈密頓算符是對易的,因而系統的波函式可以表示為y方向上動量的本徵值與諧振子本徵矢 的乘積,但 也需要在x方向上移動x,即:
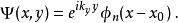 朗道規範
朗道規範總之,電子的狀態可以通過n與 k這兩個量子數表征。
朗道能級
朗道量子化所造成的效應只能在平均內能小於能級間差值,即 kT ≪ ħω時才能被觀測到。簡單來說就是溫度較低,外磁場較強。
每個朗道能級都具有一定的簡併度,因為量子數 k的取值情況為:
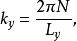 朗道規範
朗道規範式中N為整數。N所允許的取值受到振子的運動中心坐標 x的影響。振子的運動必須在系統範圍內,也就是說0 ≤ x< L。這給出了N的取值範圍:
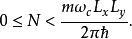 朗道規範
朗道規範對於帶電量 q= Ze的粒子來說,N的上限可以表記為磁通量的比值:
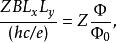 朗道規範
朗道規範式中 Φ= h/2e為磁通量的基本量子, Φ = BA是系統的磁通量,面積 A= LL。
因而對於自旋為S的粒子,每個朗道能級的簡併度的最大值D為:
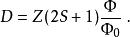 朗道規範
朗道規範上述討論只是在有限尺度內給出的粗略的結果,嚴格來說,諧振子解只對在x方向上不受限的系統有效,如果系統尺度 L是有限的,那個方向上的束縛態條件會導致磁場中的非標準量子化情況。原則上,兩個都是埃爾米特方程的解。多電子對於朗道能級的填充仍是研究熱點之一。
一般來說,朗道能級可以在電子系統中被觀察到,其中Z=1,S=1/2。隨著磁場增強,越來越多的電子會占據朗道能級。最高的朗道能級的占據情況會導致多種電子性質振盪,如德哈斯-范阿爾芬效應及舒布尼科夫-德哈斯效應。
如果考慮到塞曼效應的話,那么每個朗道能級都會分裂為一對能級:一個為自旋向上的電子占據的能級,一個是自旋向下的電子占據的能級。此時每個自旋朗道能級的簡併度就會是磁通量的比率:D= Φ/Φ。兩個能級與分裂前的能級間隔是相同的:2 μB= ħω。然而在多個能級被占滿時,系統的費米能與基態的能量卻是大致相同的,因為塞曼效應造成的影響,在這些能級相加時會被抵消掉。
討論
在上面的推導過程中,x與y似乎並不對稱。然而,考慮到系統的對稱性,並沒有物理量能表征這兩個坐標的區別。在對x與y進行適當的內部變換後,可以得到相同的結果。
此外,上述推導中電子在z方向上運動受限的情形儘管在實驗中確實存在,如二維電子氣。但這一假設並不基本。如果電子在z方向上可以自由移動,那么波函式還需要乘以一個因子exp( ikz),能量對應地需要加上( ħ k)/( 2m)。這一項會“填入”能級間隙,從而減小量子化的效果。但在垂直於磁場的平面x-y上的運動仍是量子化的。
對稱規範中的朗道能級
選定對稱規範:
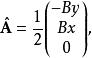 朗道規範
朗道規範對於哈密頓算符進行去量綱化:
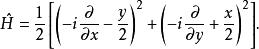 朗道規範
朗道規範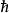 朗道規範
朗道規範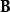 朗道規範
朗道規範實際值可以通過引入q、c、、及m等常數得出。
引入算符:
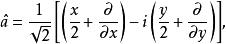 朗道規範
朗道規範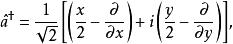 朗道規範
朗道規範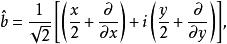 朗道規範
朗道規範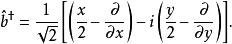 朗道規範
朗道規範這些算符的對易關係為:
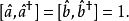 朗道規範
朗道規範哈密頓算符可記為:
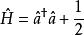 朗道規範
朗道規範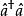 朗道規範
朗道規範朗道能級序數n是的本徵值。
角動量z方向上的分量為:
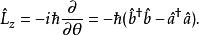 朗道規範
朗道規範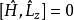 朗道規範
朗道規範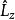 朗道規範
朗道規範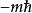 朗道規範
朗道規範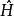 朗道規範
朗道規範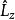 朗道規範
朗道規範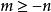 朗道規範
朗道規範利用其與哈密頓算符可對易,即,我們選定的本徵值為使與對角化的本徵函式。易見,在第n個朗道能級上存在。然而m的值可能非常大。在下面將推導系統表現出的有限簡併度。
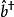 朗道規範
朗道規範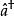 朗道規範
朗道規範使用可以使m減小一個單位同時使n保持不變,而則可以使n增大一個單位,同時令m減小一個單位。類比量子諧振子,可以得到:
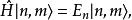 朗道規範
朗道規範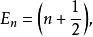 朗道規範
朗道規範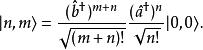 朗道規範
朗道規範在朗道規範與對稱規範下,每個朗道能級上的簡併軌道分別以量子數 k及m表征,每個朗道能級上單位面積的簡併度是相同的。
可以證明選定下面這個波函式時,也可以得到上面得到的結果:
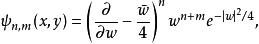 朗道規範
朗道規範 朗道規範
朗道規範式中。
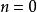 朗道規範
朗道規範 朗道規範
朗道規範特別地,對於最低的朗道能級,即時,波函式為任意一個解析函式與高斯函式的乘積:。
規範變換的影響
進行這樣的規範變換:
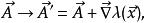 朗道規範
朗道規範運動學動量的定義為:
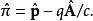 朗道規範
朗道規範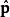 朗道規範
朗道規範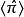 朗道規範
朗道規範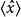 朗道規範
朗道規範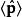 朗道規範
朗道規範式中為正則動量。哈密頓算符是規範不變的,因而與也會在規範變換後保持不變,但會受到規範變換的影響。
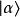 朗道規範
朗道規範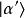 朗道規範
朗道規範為了考察規範變換帶來的影響,設磁矢勢為A與A時的量子態為與。
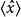 朗道規範
朗道規範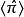 朗道規範
朗道規範由於和是規範不變的,可以得到:
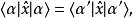 朗道規範
朗道規範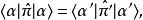 朗道規範
朗道規範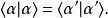 朗道規範
朗道規範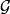 朗道規範
朗道規範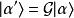 朗道規範
朗道規範設算符會使,則:
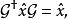 朗道規範
朗道規範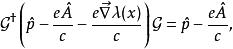 朗道規範
朗道規範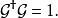 朗道規範
朗道規範綜上所述:
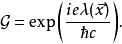 朗道規範
朗道規範參見
•物理學主題
•巴克豪森效應
•量子霍爾效應
•勞夫林波函式