定義:設函式f(x)的定義域為R.若存在與x無關的正常數M,使 |f(X) |≤M|x|對一切實數x均成立,則稱f(x)為有界泛函.
舉例
f(x)=(sinx+cosx)x
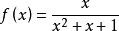 有界泛函
有界泛函"定義:設函式f(x)的定義域為R.若存在與x無關的正常數M
定義:設函式f(x)的定義域為R.若存在與x無關的正常數M,使 |f(X) |≤M|x|對一切實數x均成立,則稱f(x)為有界泛函.
舉例
f(x)=(sinx+cosx)x
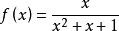 有界泛函
有界泛函泛函分析是20世紀30年代形成的數學分科,是從變分問題,積分方程和理論物理的研究中發展起來的。它綜合運用函式論,幾何學,現代數學的觀點來研究無限維向量空...
概述 拓撲線性空間 運算元 選擇公理 歷史簡介除了理想的情形以外,任何具有反饋的動力系統總是存在滯後現象;用傳統的常微分方程去描述物理系統只是一種近似,而且是有條件的,這就需要考慮帶有各種滯後量的微...
泛函微分方程 正文 相關連線局部有界空間是一類拓撲線性空間,如果拓撲線性空間E中存在零元的一個有界的鄰域,則稱E是局部有界的。局部有界空間是亥爾斯(D.H.Hyers)於1939年...
基礎概念 相關性質定理電磁場問題的泛函 變分方程 此外,抽象為運算元方程的數學模型還可轉化為等價的變分方程,使變分法可以直接用於求解方程的未知函式。
電磁場的泛函法 正文 配圖 相關連線泛函分析基礎是由劉培德所著的一本書籍,於科學出版社出版。
內容提要 編輯推薦 目錄 前言 圖書信息強制泛函是賦范線性空間中隨著範數的無限增大而一致趨向於無窮大的泛函。
簡介 泛函 賦范線性空間泛函分析是20世紀30年代形成的數學分科,是從變分問題,積分方程和理論物理的研究中發展起來的。它綜合運用函式論,幾何學,現代數學的觀點來研究無限維向量空...
學科介紹 選擇公理 歷史 拓撲線性空間 運算元《泛函分析習題集》是印度數學家V.K.Krishnan編寫的《泛函分析習題集及解答》(Textbook of Functional Analysis: ...
內容簡介 書籍介紹 目錄泛函分析中一種重要的運算元。 運算元(映射)有線性和非線性之分.線性運算元又分為有界和無界兩類,有界線性運算元是線性賦范空問的基本概念。
基本定義 舉例 相關概念 相關定理 等價形式