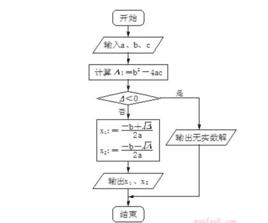
概述
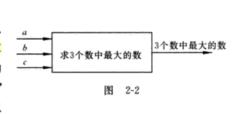 有效算法
有效算法對於那些不熟悉計算機的人來說,可以使用別人已設計好的現成算法,只需根據算法的要求給予必要的輸入,就能得到輸出的結果。對他們來說,算法如同一個“黑箱子”一樣,他們可以不了解“黑箱子”中的結構,只是從外部特性上了解算法的作用,即可方便地使用算法。例如,對一個“輸入3個數,求其中最大值”的算法,只要輸入a,b,c這三個數,執行算法後就能得到其中最大的數。但對於程式設計人員來說,必須會設計算法,並且根據算法編寫程式 。
正確認識
存在這樣一類問題,其目前最快算法所需計算次數是n的指數函式而非多項式,所以n略大時,計算機就不能勝任,故以其在計算上難於對付而聞名,被稱為NP-Complete問題,如旅行售貨員問題、時間表問題等。數學家強烈的認為:人們不可能找出一個有效算法這一事實是NP-Complete問題的固有性質。他們相信,不會有有效算法存在(如其一具有有效算法,余者皆然)。因此,對這類問題,尋找近似解的有效算法便自然成為人們追求的方向。
然而,對算法的認識並未到此結束,人們很快發現上述複雜性概念涉及到算法在最壞的情況下的性態。而這種最壞情況在實際中發生的機率究竟有多大並未予以考慮,以致出現了多項式算法反倒不如非多項式算法在實算中的奇怪現象。例如,單純形算法已被證明是普遍實用和非常有效的,但人們也舉例證明了它不是多項式算法,哈奇楊算法已被證明是多項式算法,但在許多實踐中,其計算速度反比單純性算法慢得多。這說明用算法在最壞的情況下的性態來區別好壞不是科學的,而算法的平均性態才是衡量算法好壞的最有說服力、最重要的標誌。因此,那種近憑一、兩個並不具有代表性的例子來肯定或否定一種的算法的思想和行為是不可取的。
對於解決同一類問題的各種算法,優劣立判的算法並不常見,往往是尺短寸長,各有特點。方法一可能在解決A類問題上更有效,方法二可能在解決B子類問題上更優越,應當實事求是的進行具體分析,不宜簡單肯定而否定另一種。那種認為某類問題已有有效算法,從而對新提出的算法一概採取輕視,過於挑剔甚至懷疑的態度,這對算法的發展是有害的。對算法也應採取”百花齊放,推陳出新“的方針,特別是對比較成熟的領域的算法,哪怕是稍微有所改進,也可能產生較大的經濟效益,因此更加不能忽視。
算法的發展是沒有窮盡的,人們對算法的認識也在逐漸深入,期待著有更好的好算法出現,為社會服務,為人類造福 。
其他特點
出了有效性,算法還應該具備一下特點:
1、有窮性。一個算法應包含有限的操作步驟,而不是無限的。
2、確定性。算法中的每一個步驟都應當是確定的,而不應是含糊的、模稜兩可的。
3、有零個或多個輸入。所謂輸入指在執行算法時需要從外界取得必要的信息。
4、有一個或多個輸出。算法的目的就是為了求解,”解“就是輸出。