拋射體運動

拋射體運動是以任意初速拋出的物體在地球重力作用下的運動。作這種運動的物體稱為拋射體。拋射體的質心在運動中的軌跡稱為彈道或彈道曲線。

拋射體運動

正文

以任意初速拋出的物體在地球重力作用下的運動。作這種運動的物體稱為拋射體。拋射體的質心在運動中的軌跡稱為彈道或彈道曲線。
拋射體的理想運動　指在下述四種假設下的運動：①拋射體在真空中運動；②拋射體的射程與地球的尺寸相比很小，故地球表面可視為平面，各處重力互相平行；③拋射的高度與地球半徑相比很小,各處重力加速度g可視為常數且等於在地面的值；④在地面上靜止的物體具有與地球在該點的轉動速度相同的速度，所以初速不太大時，拋射體的運動可不考慮地球的轉動。在這些假設下，拋射體對靜止於地面的直角坐標系的運動方程為：

m塯＝0，m╔＝－mg。

設初速v0與水平成θ0角，而初始條件為：

x0＝0，y0＝h，

凧0＝v0cosθ0，夻0＝v0sinθ0，

則積分後的運動方程為：

x＝v0tcosθ0，

y＝v0tsinθ0－gt2＋h，

消去t後，得彈道方程：

。

這是一個拋物線方程(圖1)。當y=h時，可從上式求出拋射體的射程：

。

可見射程不僅與初速度v0有關，且與θ0有關。當θ0=45°時，射程最大。
拋射體的實際運動　考慮空氣阻力的拋射體運動。炮彈或飛彈在空氣中運動時，空氣的阻力對彈道的影響是縮短射程、減小落地速度和增大落地角，並使彈道具有豎直漸近線（圖2）。

在阻尼介質中運動的拋射體同時受到重力P和空氣阻力R的作用（圖3）。R與速度v反向,其大小則為v的某一函式mf(v)，其中m為拋射體的質量，是為了算式簡明而寫上的。拋射體沿曲線的切向和法向的運動微分方程為：

　(1)

式中θ是速度矢量與水平軸x的夾角。
曲率半徑ρ與弧長s和傾角θ有如下關係：

，

式中負號表明θ角隨弧長s的增加而減小。於是式(1)可寫作：

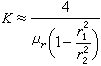。 (2)

從以上兩式消去dt，得到：

，　 (3)

或改寫為：

。 (4)

只有在函式f(v)取某些特殊形式時,式(3)才有一般的積分。例如：f(v)＝cv，f(v)＝cv2，f(v)＝av+bv2(牛頓,歐拉)，f(v)＝cvn（約翰第一·伯努利），f(v)＝a＋bvn(達朗拍）等。在外彈道學中,方程式(3)的積分一般用近似方法。下面分述介質阻力對拋射體運動的影響。
①介質阻力對射程的影響　將式(4)寫為：

。

由於,推出,即速度的水平分量是減函式,故射程比理想運動時要短。
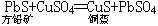②介質阻力對落地角的影響　 利用式(2)的第二式，

。　 (5)

沿彈道的上升段積分，y由0到h，θ由θ0到0，得到：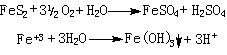

。

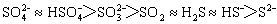如以θ1代表落地角，將式(5)沿下降段積分，得到：

。

因為vx是減函式，上面第二個積分的值必定大於第一個，故tg2θ1＞tg2θ0，即拋射體的落地角θ1大於發射角θ0。
③介質阻力對落地速度的影響將式 (2)的第一式乘以v並積分，得：

。

設落地時t＝t1，落地速度為v1,此時y＝0,上式變為：

。

此式表明v1<v0，即落地速度v1小於發射速度v0。
④阻尼介質中彈道的漸近線　θ角從初始值θ0逐漸減小，在彈道頂點處變為零,此後即取負值。由式(2)中的第二式得出：

，

根據初始條件t＝0時θ＝θ0，積分後可得：

。

從上式可以看出，當θ→時，t→∞,故在阻尼介質中彈道具有豎直漸近線。
此外，當射程較大時,例如遠程彈道飛彈,由於地面是球形,球面曲率的影響是增大射程（圖4）。圖中橢圓是飛彈在地球有心力場中的真空彈道。此時的射程等於Rφ，顯然大於設地面為平面情況下的射程。

配圖

相關連線