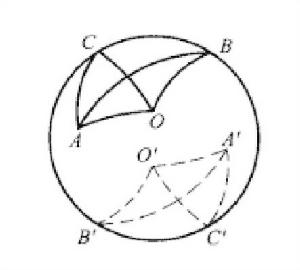
相關概念
1. 連球面上兩點的大圓劣弧稱為這兩點的球面距離。
2. 球面上相交的兩個大圓弧所在半平面之間所成的二面角稱為球面角,當球面角是直角時稱為直球面角,兩個有共同直徑的大圓弧之間所夾的球面部分稱為球面弓月形,球面弓月形所對的球面角稱為月形角。
3. 過球面一點與圓面垂直的大圓夾在該點與該圓之間最小的那段弧稱為點與圓面的球面距離。
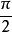 球面多邊形
球面多邊形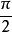 球面多邊形
球面多邊形4. 垂直於圓面的球直徑,稱為這個圓的軸,軸的端點稱為圓的極,由極至0圓的球面距離大圓弧的弧度稱為極距,極距是 的圓弧又稱為該極的極線,若且唯若圓是大圓時距它的極為 ;反之,極線必須是大圓弧。
5. 由球面小圓周上的點到它的極的球面距離,稱為該小圓的球面半徑。
6. 球面若干個大圓劣弧圍成的球面的一部分稱為球面多邊形,各大圓弧稱為球面多邊形的邊,以其弧度度量邊的大小:相鄰兩條大圓弧所成的球面角稱為球面多邊形的內角(簡稱為球面多邊形的角),同一大圓弧的球面多邊形的內角的鄰角稱為球面多邊形的外角,根據球面多邊形的邊數我們稱球面多邊形為球面三角形、球面四邊形、球面五邊形等。
7. 把一個球面多邊形任意一邊向兩方無限延長成大圓,如果其餘邊都在此大圓的同旁,那么這個多邊形就稱為球面凸多邊形。
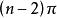 球面多邊形
球面多邊形8. 球面凸禮邊形的內角和與 的差稱為球面凸n邊形的球面角盈,通常用E來表示球面角盈。
9. 過球面線段中點,且垂直於這條球面線段的大圓稱為這條球面線段的垂直平分線或中垂線。
10. 設球面多角形每個頂點在一球面小圓周上,則該小圓稱為球面多邊形的球面外接圓。
11. 平分球面角的大圓稱為球面角的平分線,類似平面角平分線的證明,可得
12. 設一球面小圓周與多邊形各邊所在大圓相切,若該小圓在球面多邊形內部,則稱為球面多邊形的球面內切圓。
相關定理
定理1. 經過球面上兩點並且曲線上每點都在球面上的所有曲線中,以大圓的劣弧的長度最小。
 球面多邊形
球面多邊形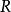 球面多邊形
球面多邊形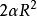 球面多邊形
球面多邊形定理2. 如果月形角是 ,球半徑是 ,則球面弓月形的面積等於 。
定理3. 設球面小圓的球面半徑是r,球的半徑是R,則小圓所在平面截球面所得的球冠的面積是
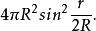 球面多邊形
球面多邊形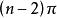 球面多邊形
球面多邊形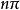 球面多邊形
球面多邊形定理4. 球面凸n邊形的角大於 ,且小於 。
 球面多邊形
球面多邊形定理5. n(n是整數,n≥3)條邊能構成球面凸n邊形的充要條件是這些邊的和小於 ,且任意一邊小於其他邊的和。
定理6. 給定凸n(n是整數,n≥4)邊形的邊,則這個凸n邊形有無數個。
定理7. 球面線段的垂直平分線上的點到這條線段兩端點的球面距離相等。
定理8.球面多邊形若有外接圓,則外接圓圓心是各邊垂直平分線的交點。
定理9. 球面三角形必定有外接圓。
定理10.球面角的平分線上的點到球面角兩邊的球面距離相等。
定理11. 球面多邊形若有內切圓,則內切圓圓心是各角平分線的交點。
定理12. 球面三角形必定有內切圓。
面積計算
球面三角形的面積是它的角的和與π的差。
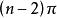 球面多邊形
球面多邊形n邊球面多邊形的面積,是它的角的和與 的差。