簡介
二階變分
二階變分是泛函沿任一函式方向的二階微分。
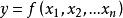附屬變分問題
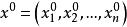附屬變分問題n元二次可微數值函式 在穩定點 取極小值的必要條件是黑塞矩陣
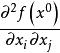附屬變分問題半正定，而此黑塞矩陣正定是 f 在穩定點x 取極小值的充分條件，與此類似，為討論泛函的平穩函式取極值的必要條件和充分條件，也需引進泛函的二階變分，以及相應泛函在平穩函式取極值的判別法，對於給定的泛函
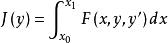附屬變分問題
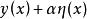附屬變分問題如果用 代替泛函 J 的被積表達式中的 y 得J(α)，泛函 J 的二階變分相應於J(α) 按α冪的展開式中含α 的那個項的係數，記J的二階變分為δ J，即
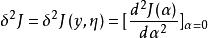附屬變分問題對於泛函 J(y) 有
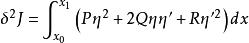附屬變分問題
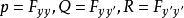附屬變分問題其中 或
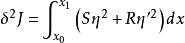附屬變分問題
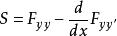附屬變分問題定義
對於泛函
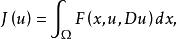附屬變分問題
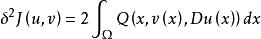附屬變分問題其中
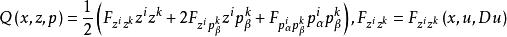附屬變分問題
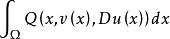附屬變分問題它們與泛函ℒ(v)=對應的變分問題稱為附屬變分問題。
變分問題
變分問題(variational problem)是有關求泛函的極大值和極小值的問題。最早研究的重要變分問題有：
1、最速降線問題：給定不在同一鉛垂線上的兩點A和B，求出連結A和B的一條曲線使其具有這樣的性質：當質點受重力作用沿著這條曲線由A下滑至B時所需時間為最少。
2、短程線問題：求曲面φ(x,y,z)=0上所給二點間長度最短的曲線，這條最短曲線稱為短程線或測地線。
3、基本的等周問題：求長為一定的封閉曲線l，使其所圍的面積S為極大。
