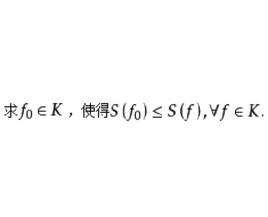最小曲面問題
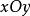 變分問題
變分問題 變分問題
變分問題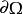 變分問題
變分問題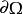 變分問題
變分問題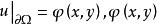 變分問題
變分問題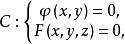 變分問題
變分問題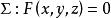 變分問題
變分問題設 平面上的開區域 ,其邊界記為 ,在 上給定函式值 是已知函式,於是得到一空間曲線 其中曲面 正是所要求的曲面,此曲面要求滿足的條件是由曲線C在空間中所張成的曲面面積最小。
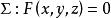 變分問題
變分問題 變分問題
變分問題由微積分的知識可以推導出曲面 在開區域 上的面積表達式。
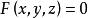 變分問題
變分問題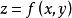 變分問題
變分問題不妨假設函式 滿足隱函式存在定理的條件,則有 ,並且曲面的面積可表示為
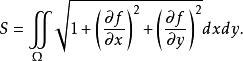 變分問題
變分問題 變分問題
變分問題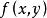 變分問題
變分問題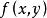 變分問題
變分問題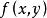 變分問題
變分問題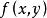 變分問題
變分問題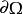 變分問題
變分問題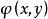 變分問題
變分問題很顯然,當給定不同的 時,面積S是不同的。曲面面積是關於函式 的函式,稱面積S是函式 的泛函.函式 必須滿足如下條件:①存在連續的一階偏導數;② 在邊界 必須與 相等。用集合的概念描述為
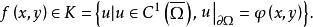 變分問題
變分問題於是,求最小曲面問題就可以轉化為如下泛函極值的問題 :
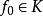 變分問題
變分問題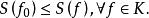 變分問題
變分問題求 ,使得
最速降線問題
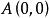 變分問題
變分問題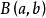 變分問題
變分問題求質點的運動軌跡曲線,質量為m的質點在重力的作用下,沿此光滑曲線無摩擦運動,使質點從點下降到點的速度最快或者時間最短。
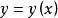 變分問題
變分問題設任意一條過A,B兩點的曲線的方程為,點P是曲線上的任意一點,設質點
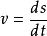 變分問題
變分問題過此點的速率是,由能量守恆有
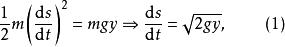 變分問題
變分問題其中s是質點所走過的路程,即從A點到P點的弧長,由弧微分公式:
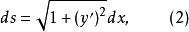 變分問題
變分問題把式(2)代人式(1)有
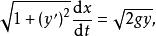 變分問題
變分問題或者
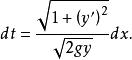 變分問題
變分問題對上式兩邊進行積分,得到從A點到B點的時間為
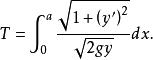 變分問題
變分問題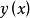 變分問題
變分問題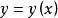 變分問題
變分問題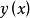 變分問題
變分問題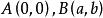 變分問題
變分問題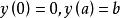 變分問題
變分問題顯然,選擇不同的路徑曲線,得到時間是不同的,即時間T是路徑的函式。曲線要滿足如下條件:①函式存在一階導數;②點必須存曲線上,即,用集合的概念描述為
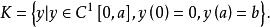 變分問題
變分問題於是,求最速下降問題就可以轉化為如下泛函極值的問題 :
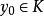 變分問題
變分問題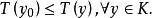 變分問題
變分問題求, 使得
等周問題
 變分問題
變分問題存周長為的所有在平面上光滑的封閉曲線中,求所圍面積最大的曲線。
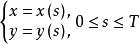 變分問題
變分問題設封閉曲線的參數方程為,由弧長公式知曲線方程應該滿足如下方程:
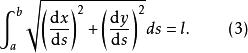 變分問題
變分問題由封閉曲線所圍成的面積公式有
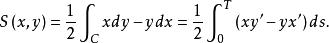 變分問題
變分問題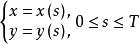 變分問題
變分問題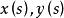 變分問題
變分問題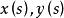 變分問題
變分問題曲線要滿足:①函式存在一階導數;②函式滿足式(3)。用集合的概念描述為
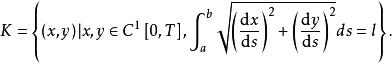 變分問題
變分問題於是,等周問題轉化為如下泛函極值的問題
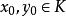 變分問題
變分問題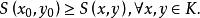 變分問題
變分問題求, 使得
短程線問題
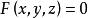 變分問題
變分問題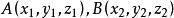 變分問題
變分問題求在曲面上給定兩點之間最短曲線的方程。比如,球面上任意兩點之間的球面上距離最短的曲線就是過這兩點的大圓的劣弧。
 變分問題
變分問題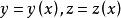 變分問題
變分問題設為參數,曲面上的光滑曲線用參數方程表示,那么過A,B兩點的曲線長度為
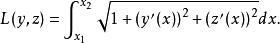 變分問題
變分問題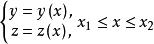 變分問題
變分問題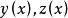 變分問題
變分問題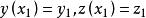 變分問題
變分問題曲線要滿足:①函式存在一階導數;②函式滿足。用集合的概念描述為
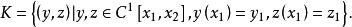 變分問題
變分問題於是,短程線問題轉化為如下泛函極值的問題:
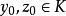 變分問題
變分問題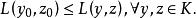 變分問題
變分問題求, 使得
總結上面四個實際問題的例子,都是研究泛函在某個集合上的極值問題.這就是古典變分問題 。