定義
在尺度空間M中給定一個點集S和一個目標點q ∈ M,在S中與q距離最近的點即為點q的最鄰近點。很多情況下,M為多維的歐幾里得空間,距離由歐幾里得距離或曼哈頓距離決定。
最鄰近點搜尋
線性查找
遍歷整個點集,計算它們和目標點之間的距離,同時記錄目前的最近點。這樣的算法較為初級,可以為較小規模的點集所用,但是對於點集的尺寸和空間的維數稍大的情況不適用。
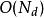 最近鄰點
最近鄰點線性查找所需時間為,其中N是S的勢,d是S的維。由於不需要建立數據結構,所以線性查找沒有存儲空間複雜度的問題。
空間分割
從七十年代起分支限界方法被套用於這個問題。對歐幾里得空間來說,這個方法被稱為空間索引或者空間訪問方法。目前已發展出好幾種分支限界方法。恐怕最簡單的當屬Kd樹,它將查找空間不斷將父節點包含的區域分為相鄰的兩部分,每部分包含原來區域中的一半點。求解時,從根節點開始在每個分叉點上對目標點進行計算,直到葉節點。對於給定的維度,查找時間複雜度為O(logN)。R樹數據結構能高效插入和刪除節點,用來解決動態環境下的最鄰近搜尋。
對於一般的度量空間,分支限界方法被稱為度量樹,特別的例子有VP樹和Bk樹。
局部敏感哈希(LSH)
LSH(localitysensitivehashing)通過對點進行某種度量操作後將點分組散列在不同的次點集中。在這種度量下相互間距離較近的點被分在同一個次點集的可能性較高。
局部敏感哈希的基本思想:在高維數據空間中的兩個相鄰的數據被映射到低維數據空間中後,將會有很大的機率任然相鄰;而原本不相鄰的兩個數據,在低維空間中也將有很大的機率不相鄰。通過這樣一映射,我們可以在低維數據空間來尋找相鄰的數據點,避免在高維數據空間中尋找,因為在高維空間中會很耗時。有這樣性質的哈希映射稱為是局部敏感的。
K最近鄰分類算法
K最近鄰(k-Nearest Neighbor,KNN)分類算法,是一個理論上比較成熟的方法,也是最簡單的機器學習算法之一。該方法的思路是:如果一個樣本在特徵空間中的k個最相似(即特徵空間中最鄰近)的樣本中的大多數屬於某一個類別,則該樣本也屬於這個類別。
KNN是通過測量不同特徵值之間的距離進行分類。它的的思路是:如果一個樣本在特徵空間中的k個最相似(即特徵空間中最鄰近)的樣本中的大多數屬於某一個類別,則該樣本也屬於這個類別。K通常是不大於20的整數。KNN算法中,所選擇的鄰居都是已經正確分類的對象。該方法在定類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。
其算法的描述為:
1)計算測試數據與各個訓練數據之間的距離;
2)按照距離的遞增關係進行排序;
3)選取距離最小的K個點;
4)確定前K個點所在類別的出現頻率;
5)返回前K個點中出現頻率最高的類別作為測試數據的預測分類。
套用示例(郵局問題)
問題描述:
在一個按照東西和南北方向劃分成規整街區的城市裡,n個居民點散亂地分布在不同的街區中。用x 坐標表示東西向,用y坐標表示南北向。各居民點的位置可以由坐標(x,y)表示。街區中任意2 點(x1,y1)和(x2,y2)之間的距離可以用數值|x1-x2|+|y1-y2|度量。居民們希望在城市中選擇建立郵局的最佳位置,使n個居民點到郵局的距離總和最小。
編程任務:
給定n 個居民點的位置,編程計算n 個居民點到郵局的距離總和的最小值。
解題思路:
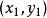 最近鄰點
最近鄰點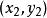 最近鄰點
最近鄰點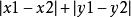 最近鄰點
最近鄰點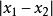 最近鄰點
最近鄰點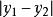 最近鄰點
最近鄰點因為街區中任意2 點和之間的距離可以用數值度量,所以我們可以將任意2點的距離可以看作為x坐標上的距離和y坐標的距離之和。可以將這個2維的題目拆分為2個一維,然後將它們合併。
1) 找出x坐標(此時可忽略y坐標)的最優點,最優點是中點,可以用:a)線性時間找中位數;b)先排序在找中位數
2)找出y坐標(此時可忽略x坐標)的最優點,最優點是中點,可以用: a)線性時間找中位數;b)先排序在找中位數
3)合併,將x ,y坐標所求的距離和相加即是最有值。
