Knn[最鄰近結點算法]

鄰近算法，或者說K最近鄰(kNN，k-NearestNeighbor)分類算法是數據挖掘分類技術中最簡單的方法之一。所謂K最近鄰，就是k個最近的鄰居的意思，說的是每個樣本都可以用它最接近的k個鄰居來代表。

kNN算法的核心思想是如果一個樣本在特徵空間中的k個最相鄰的樣本中的大多數屬於某一個類別，則該樣本也屬於這個類別，並具有這個類別上樣本的特性。該方法在確定分類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。 kNN方法在類別決策時，只與極少量的相鄰樣本有關。由於kNN方法主要靠周圍有限的鄰近的樣本，而不是靠判別類域的方法來確定所屬類別的，因此對於類域的交叉或重疊較多的待分樣本集來說，kNN方法較其他方法更為適合。

簡介

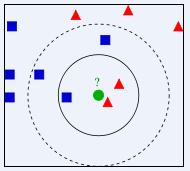KNN算法的決策過程

右圖中，綠色圓要被決定賦予哪個類，是紅色三角形還是藍色四方形？如果K=3，由於紅色三角形所占比例為2/3，綠色圓將被賦予紅色三角形那個類，如果K=5，由於藍色四方形比例為3/5，因此綠色圓被賦予藍色四方形類。

K最近鄰(k-Nearest Neighbor，KNN)分類算法，是一個理論上比較成熟的方法，也是最簡單的機器學習算法之一。該方法的思路是：如果一個樣本在特徵空間中的k個最相似(即特徵空間中最鄰近)的樣本中的大多數屬於某一個類別，則該樣本也屬於這個類別。KNN算法中，所選擇的鄰居都是已經正確分類的對象。該方法在定類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。 KNN方法雖然從原理上也依賴於極限定理，但在類別決策時，只與極少量的相鄰樣本有關。由於KNN方法主要靠周圍有限的鄰近的樣本，而不是靠判別類域的方法來確定所屬類別的，因此對於類域的交叉或重疊較多的待分樣本集來說，KNN方法較其他方法更為適合。

KNN算法不僅可以用於分類，還可以用於回歸。通過找出一個樣本的k個最近鄰居，將這些鄰居的屬性的平均值賦給該樣本，就可以得到該樣本的屬性。更有用的方法是將不同距離的鄰居對該樣本產生的影響給予不同的權值(weight)，如權值與距離成反比。

算法流程

1. 準備數據，對數據進行預處理

2. 選用合適的數據結構存儲訓練數據和測試元組

3. 設定參數，如k

4.維護一個大小為k的的按距離由大到小的優先權佇列，用於存儲最近鄰訓練元組。隨機從訓練元組中選取k個元組作為初始的最近鄰元組，分別計算測試元組到這k個元組的距離，將訓練元組標號和距離存入優先權佇列

5. 遍歷訓練元組集，計算當前訓練元組與測試元組的距離，將所得距離L 與優先權佇列中的最大距離Lmax

6. 進行比較。若L>=Lmax，則捨棄該元組，遍歷下一個元組。若L < Lmax，刪除優先權佇列中最大距離的元組，將當前訓練元組存入優先權佇列。

7. 遍歷完畢，計算優先權佇列中k 個元組的多數類，並將其作為測試元組的類別。

8. 測試元組集測試完畢後計算誤差率，繼續設定不同的k值重新進行訓練，最後取誤差率最小的k 值。

優點

1.簡單，易於理解，易於實現，無需估計參數，無需訓練；

2. 適合對稀有事件進行分類；

3.特別適合於多分類問題(multi-modal,對象具有多個類別標籤)， kNN比SVM的表現要好。

缺點

該算法在分類時有個主要的不足是，當樣本不平衡時，如一個類的樣本容量很大，而其他類樣本容量很小時，有可能導致當輸入一個新樣本時，該樣本的K個鄰居中大容量類的樣本占多數。 該算法只計算“最近的”鄰居樣本，某一類的樣本數量很大，那么或者這類樣本並不接近目標樣本，或者這類樣本很靠近目標樣本。無論怎樣，數量並不能影響運行結果。

該方法的另一個不足之處是計算量較大，因為對每一個待分類的文本都要計算它到全體已知樣本的距離，才能求得它的K個最近鄰點。

可理解性差，無法給出像決策樹那樣的規則。

改進策略

kNN算法因其提出時間較早，隨著其他技術的不斷更新和完善，kNN算法的諸多不足之處也逐漸顯露，因此許多kNN算法的改進算法也應運而生。

針對以上算法的不足，算法的改進方向主要分成了分類效率和分類效果兩方面。

分類效率：事先對樣本屬性進行約簡，刪除對分類結果影響較小的屬性，快速的得出待分類樣本的類別。該算法比較適用於樣本容量比較大的類域的自動分類，而那些樣本容量較小的類域採用這種算法比較容易產生誤分。

分類效果：採用權值的方法（和該樣本距離小的鄰居權值大）來改進，Han等人於2002年嘗試利用貪心法，針對檔案分類實做可調整權重的k最近鄰居法WAkNN (weighted adjusted k nearest neighbor)，以促進分類效果；而Li等人於2004年提出由於不同分類的檔案本身有數量上有差異，因此也應該依照訓練集合中各種分類的檔案數量，選取不同數目的最近鄰居，來參與分類。