特點
方向可調濾波器具有任意旋轉的功能，並可簡單地表示為一組基濾波器的線性組合。由這種濾波器及其 Hilbert 變換形成的正交濾波器組，可以準確地檢測出目標的邊緣、紋理以及奇異點等特徵。
結構
方向可調濾波器對應的濾波器基是在頻域上相互之間有一定重疊的一組濾波器，其中的每一個基濾波器都可表示為方向可調濾波器旋轉到某一角度時的形式。在這裡，選取二維高斯函式的一階導數作為“基濾波器”，如下式所示：
方向可調濾波器
方向可調濾波器
方向可調濾波器式（1）為高斯函式，式（2）為 0°方向的基濾波器，式（3）為 90°方向的基濾波器，對（2）和（3）進行線性組合，即可得到任意方向的濾波輸出，如下式所示：
方向可調濾波器
方向可調濾波器其中， 是方向可調濾波器的方向輸入。
套用
消噪
假定源圖像中混有一定的加性孤立噪聲，這種噪聲往往是一些單像素奇異點。對這些奇異點，可以採用全局中值濾波的方法來剔除，但這種方法存在一個弱點，即在消除噪聲點的同時，也削弱了圖像中的特徵。如果對圖像進行一次預處理，找出圖像中可能的噪聲點，從而只在這些噪聲點處進行局部中值濾波，那么源圖像的特徵可以較好地保存下來，而絕大部分噪聲被濾去。
根據方向可調濾波器的原理，在圖像中同時滿足以下2個條件的，可以判定為孤立噪聲點。
（1）由於噪聲點與特徵一樣，也具有較大的奇異性，因此其局部方向能量很大。
（2）對於孤立噪聲點，由於不具備很強的方向性，因而各個方向上的方向能量相差不大。即在孤立噪聲點，方向能量的最小值與最大值之間比較接近。如果使用上節中設計的方向可調濾波器來分析每幅源圖中的方向能量，則在各個噪聲點處，與最小方向能量對應的方向垂直於主要方向。
邊緣檢測
邊緣檢測是最早套用的圖像分割方法。它通過檢測圖像上不同區域交界處的亮度變化實現圖像中不同對象的分割。按數據的處理順序可以將邊緣檢測方法分為串列方法和並行方法。前者從特定的初始點的鄰域中按一定方向和規則尋找邊緣點，再將找到的邊緣點作為新的初始點繼續尋找，重複這一過程可以得到連續的邊緣線條。後者則僅憑藉目標點及其周圍若干像素的亮度來判斷邊緣點。
梯度計算法是最簡單的邊緣檢測方法，它利用方嚮導數濾波器計算圖像梯度藉以判斷邊緣位置，是一種並行方法。經典的梯度運算元如Sobel運算元，根據其直觀意義給出在相隔90°的兩個基本方向上運算元，如下圖：
圖1 0°和90°方向上的Sobel運算元在這種情況下,為了得到其他方向上的方嚮導數，需要使用矢量合成的方法。其原理如下：
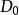方向可調濾波器
方向可調濾波器 方向可調濾波器分別利用0°和90°方向上的運算元計算兩個方向上的方嚮導數，分別記作和，則方向上的方嚮導數計算值為：
方向可調濾波器
方向可調濾波器梯度大小的計算值為：
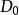方向可調濾波器 方向可調濾波器
方向可調濾波器求和都需要對於整幅圖像進行模板運算，所以用這種方式求取就需要兩次模板運算。模板運算的運算量相當大，由此產生了直接計算任意方向上的方嚮導數的需求。滿足這一需求的方法是直接構造任意方向上的方嚮導數濾波器，如Kirsch濾波器，具有8個基本方向。
Matlab代碼
clc;
close all;
clear all;
theta = [0:15:360];
inImg = imread('example.png');
dim = ndims(inImg);
if(dim == 3)
%Input is a color image
inImg = rgb2gray(inImg);
end
I = inImg;
tic
for i = [1:length(theta)]
J1(:,:,i) = steerGaussFilterOrder1(I,theta(i),3,true);
end
toc
tic
for i = [1:length(theta)]
J2(:,:,i) = steerGaussFilterOrder2(I,theta(i),3,true);
end
toc
