定義
![梯度[數學名詞]](/img/0/e61/wZwpmL2UTO4AzMxgDNxMDN0UTMyITNykTO0EDMwAjMwUzL4QzLwUzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/f/269/wZwpmLxMzNyATO3gDN2IDN0UTMyITNykTO0EDMwAjMwUzL4QzLzAzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/0/e61/wZwpmL2UTO4AzMxgDNxMDN0UTMyITNykTO0EDMwAjMwUzL4QzLwUzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/f/7ce/wZwpmL1ETN4IzN4ATO4EDN0UTMyITNykTO0EDMwAjMwUzLwkzLyMzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]設二元函式 在平面區域D上具有一階連續偏導數,則對於每一個點P(x,y)都可定出一個向量 ,該函式就稱為函式 在點P(x,y)的梯度,記作gradf(x,y)或 ,即有:
![梯度[數學名詞]](/img/f/7ce/wZwpmL1ETN4IzN4ATO4EDN0UTMyITNykTO0EDMwAjMwUzLwkzLyMzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/f/269/wZwpmLxMzNyATO3gDN2IDN0UTMyITNykTO0EDMwAjMwUzL4QzLzAzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]gradf(x,y)= =
![梯度[數學名詞]](/img/3/80a/wZwpmL4EDMwUTMwMzMzIDN0UTMyITNykTO0EDMwAjMwUzLzMzL2MzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/f/beb/wZwpmLwUjMzQDO1cjN1IDN0UTMyITNykTO0EDMwAjMwUzL3YzL2gzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]其中 稱為(二維的)向量微分運算元或Nabla運算元, 。
![梯度[數學名詞]](/img/5/c16/wZwpmLyYTO2QDM4kTNwMDN0UTMyITNykTO0EDMwAjMwUzL5UzLxAzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]設 是方向l上的單位向量,則
![梯度[數學名詞]](/img/d/d26/wZwpmL2gDNwIDN1EDNxMDN0UTMyITNykTO0EDMwAjMwUzLxQzL0czLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/1/9a9/wZwpmL3gDM3MzMwITN2IDN0UTMyITNykTO0EDMwAjMwUzLyUzL2UzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]由於當方向l與梯度方向一致時,有
![梯度[數學名詞]](/img/a/8b8/wZwpmL4QzNzIjM2MzNwIDN0UTMyITNykTO0EDMwAjMwUzLzczL0EzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/a/284/wZwpmLyMTO1MTNyUjNxIDN0UTMyITNykTO0EDMwAjMwUzL1YzL1QzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]所以當l與梯度方向一致時,方嚮導數 有最大值,且最大值為梯度的模,即
![梯度[數學名詞]](/img/e/1e7/wZwpmLxAjNxIDM3ITM0EDN0UTMyITNykTO0EDMwAjMwUzLyEzLxczLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]因此說,函式在一點沿梯度方向的變化率最大,最大值為該梯度的模。
推廣
梯度的概念可以推廣到三元函式的情形。
![梯度[數學名詞]](/img/2/eb0/wZwpmL4gTN1MzM1MjN1ATN0UTMyITNykTO0EDMwAjMwUzLzYzL1MzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/d/159/wZwpmL4YDNykjNzMjM0EDN0UTMyITNykTO0EDMwAjMwUzLzIzL0MzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]設三元函式 在空間區域G內具有一階連續偏導數,點 ,稱向量
![梯度[數學名詞]](/img/9/723/wZwpmL1AzM2UTO4UDM5IDN0UTMyITNykTO0EDMwAjMwUzL1AzL3QzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/2/eb0/wZwpmL4gTN1MzM1MjN1ATN0UTMyITNykTO0EDMwAjMwUzLzYzL1MzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/d/685/wZwpmL3cDO4EzNwMzNxIDN0UTMyITNykTO0EDMwAjMwUzLzczL0gzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/d/0e4/wZwpmL4cjN3kDNzMjM0EDN0UTMyITNykTO0EDMwAjMwUzLzIzL1MzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]為函式 在點P的梯度,記為 或 ,即
![梯度[數學名詞]](/img/d/685/wZwpmL3cDO4EzNwMzNxIDN0UTMyITNykTO0EDMwAjMwUzLzczL0gzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/d/0e4/wZwpmL4cjN3kDNzMjM0EDN0UTMyITNykTO0EDMwAjMwUzLzIzL1MzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/9/313/wZwpmL2ETOzEDOxUjNxIDN0UTMyITNykTO0EDMwAjMwUzL1YzL1AzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]==
![梯度[數學名詞]](/img/3/6a2/wZwpmL4ATN2gTM2MzNwIDN0UTMyITNykTO0EDMwAjMwUzLzczLzAzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]![梯度[數學名詞]](/img/6/1bd/wZwpmLxMzM3UzNyMTMzEDN0UTMyITNykTO0EDMwAjMwUzLzEzLxUzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 梯度[數學名詞]
梯度[數學名詞]其中稱為(三維的)向量微分運算元或Nabla運算元,。
同樣,該梯度方向與取得最大方嚮導數的方向一致,而它的模為方嚮導數的最大值。
套用
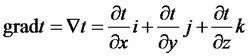 溫度梯度的表達式
溫度梯度的表達式設體系中某處的物理參數(如溫度、速度、濃度等)為w,在與其垂直距離的dy處該參數為w+dw,則稱為該物理參數的 梯度,也即該物理參數的變化率。如果參數為速度、濃度、溫度或空間,則分別稱為速度梯度、濃度梯度、溫度梯度或空間梯度。其中溫度梯度在直角坐標系下的表達式如右圖。
在向量微積分中,標量場的 梯度是一個向量場。標量場中某一點上的梯度指向標量場增長最快的方向,梯度的長度是這個最大的變化率。更嚴格的說,從歐幾里得空間 R n到 R的函式的梯度是在 R n某一點最佳的線性近似。在這個意義上,梯度是雅可比矩陣的特殊情況。
在單變數的實值函式的情況, 梯度只是導數,或者,對於一個線性函式,也就是線的斜率。
梯度一詞有時用於 斜度,也就是一個曲面沿著給定方向的 傾斜程度。可以通過取向量梯度和所研究的方向的點積來得到斜度。梯度的數值有時也被稱為梯度。
![梯度[數學名詞] 梯度[數學名詞]](/img/7/e1f/nBnauM3X2YTN2UTNzMDO2IDN0UTMyITNykTO0EDMwAjMwUzLzgzLxUzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg)
