基本介紹
斜線長定理 從平面外一點向這個平面所引的垂線段和斜線段中:
1.射影相等的兩條斜線段相等;
2.射影不等的兩條斜線段中,射影較長的斜線段較長;
3.垂線段比任何一條斜線段都短。
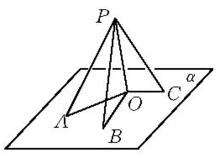 圖1
圖1斜線長定理的證明
斜線長定理是指自平面外一點引這平面的兩條斜線和一條垂線,則投影相等,斜線長也相等;投影較長,斜線長也較長 。
證明 設AB⊥α,AC、AD、AE是從點A到平面α的斜線,且BC=BD,BE>BC(見圖2)。
 圖2
圖2∵AB⊥α,
∴AB⊥BC,AB⊥BD,AB⊥BE,
(1)在直角三角形ABC及ABD中
∵BC=BD,AB為公共邊
∴△ABC≌△ABD,則AC= AD。
(2)∵BE> BC,在BE上截取BF= BC,連線AF
∵BF=BC,
∴AF=AC。
在AB和AE所作的平面內因∠AFE>90°,
∴AE>AF,因而AE>AC 。
斜線長定理的逆定理
射影長定理是斜線長定理的逆定理。
從平面外一點向這平面引一條垂線和若千條斜線:
(1)相等斜線的射影相等;
(2)較長斜線的射影較長。
例題解析
【例1】P是直角△ABC所在平面外一點,且PA=PB= PC,又O是斜邊AB的中點,求證:PO⊥平面ABC。
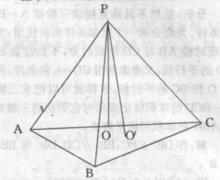 圖3
圖3證明:作PO'⊥平面ABC於O'。
∵PA= PB=PC,由斜線長定理可知:AO'=BO' =CO' ,即O'是△ABC的外心。又由已知O是△ABC斜邊AB的中點可知,O是△ABC的外心,
∴O與O'重合故PO'與PO重合,
∴PO⊥平面ABC。
說明:此題用直線與平面垂直的判定定理亦可證明,但不如用“同一法”證明簡捷 。