斜二測法

斜二測法是空間幾何體直觀圖的一種畫法。

基本信息

• 解釋：三維空間到二維空間的投影
• 意義：空間幾何體直觀圖的一種畫法

事實上，斜二測畫法是三維空間到二維空間的投影，但由於圓本身是二維圖形，所以這圖形的變換還是二維到二維的。我們也就不必再去想相對複雜的立體問題，只把它看作是平面圖形的變換。

用高等一點的語言說：因為容易看出斜二測畫法保持線段長度的比例不變，從而也就保持平行關係，所以它是一個仿射變換。由於二次曲線在仿射變換下不改變類型，所以圓（可看成特殊的橢圓）仍被變成橢圓。

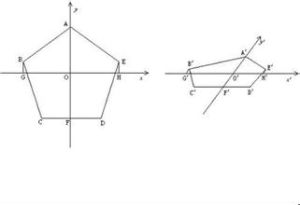
這是空間幾何體直觀圖的一種畫法

畫法

（1）在已知圖像中取互相垂直的x軸和y軸，兩軸相交於點O，畫直觀圖時，畫出相應的x′ 軸和y′ 軸，兩軸相交於O′，且使∠x′O′y′=45° 或135° ，它們確定的平面表示水平面。

（2）已知圖形中平行於x軸或y軸的線段，在直觀圖中分別畫出平行於x′ 軸和y′ 軸的線段。

（3）已知圖形中平行於x軸的線段在直觀圖中長度保持不變，平行於y軸的線段長度變成原來的一半。

面積比

水平放置的正方形的面積與斜二測畫法所得的直觀圖是一個四邊形，兩者面積之比為2√2∶1