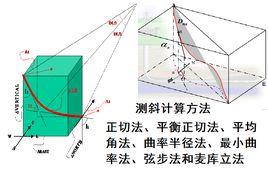
測斜計算的方法
測斜計算的方法可分為兩大類二十多種。一類是把井眼軸線視為由很多直線段組成，另一類則視其為不同曲率半徑的圓弧組成。計算方法多種多樣，測段形狀不可確定。主要的計算方法有正切法、平衡正切法、平均角法、曲率半徑法、最小曲率法、弦步法和麥庫立法。從計算精度來講，最高的是曲率半徑法和最小曲率法，其次是平均角法。下各圖和計算公式中下角符號1、2分別代表上測點和下測點。
1.平均角法（角平均法）
平均角法（THE AVERAGE ANGLE method）
此法認為兩測點間的測段為一條直線，該直線的方向為上下兩測點處井眼方向的矢量和方向。
測段計算公式：
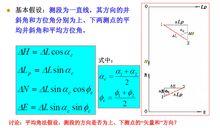測斜計算方法特殊情況的考慮：
* 在上下兩測點中，若上測點的井斜角I1=0，則Ac=a2；
* 在上下兩測點中，若下測點的井斜角I2=0，則Ac=a1；
l方位角選用圓周方位，即0－360º，△EAST為負值時表示"西"；△NORTH 為負值時表示"南"。
l如果│a2-a1│>180°時，要正確判斷其平均方位：
其表達式為：Ac=[360-ABS(a2-a1)]/2+a2
2．平衡正切法
此法假定二測點間的井段為兩段各等於測段長度一半的直線構成的折線，它們的方向分別與上、下兩測點處的井眼方向一致。
計算式為：
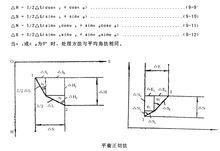測斜計算方法3. 曲率半徑法（圓柱螺線法）
此法假設兩測點間的測段是條等變螺旋角的圓柱螺線，螺線在兩端點處與上、下二測點處的井眼方向相切。
如圖9－7，測段的計算公式有三種表達形式。
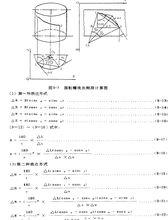測斜計算方法（1）第一種表達形式
測斜計算方法（9－13）～（9－16）式中：
測斜計算方法這四個公式是最常用的計算公式：
（3）第三種表達形式
（4）曲率半徑法的特殊情況處理
測斜計算方法③第三種特殊情況，α≠α，且其中之一等於零。此時，按二測點方位角相等來處理，然後代入第二種特殊情況的計算式中。
4．最小曲率法
最小曲率法假設兩測點間的井段是一段平面的圓弧，圓弧在兩端點處與上下二測點處的井眼方向線相切。測段計算如圖9－8。
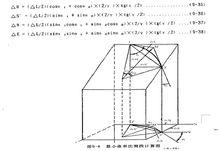測斜計算方法測段計算公式右：
令f=（2/γ）×tg（γ/2），f是個大於1但很接近1的值。在狗腿角γ足夠小的情況下，可近似認為f=1，這時上述四個計算公式就完全變成平衡正切法的公式了，它是對平衡正切法公式的校正。
ΔS′是切線1M和M2在水平面上的投影之和，即ΔS′=1′M′+M′2′。ΔS′並不是測段的水平投影長度ΔS。要作出井身垂直剖面圖，需要求出ΔS，而最小曲率法卻求不出ΔS，這是最小曲率法的缺點。為了作出垂直剖面圖，可用下式近似地求出ΔS′：
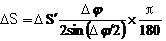測斜計算方法其它與測斜計算相關參數
1. 井深 （或稱為斜深、測深）井口(通常以轉盤面為基準)至測點的井眼長度。以字母L表示，單位為 米(m)。
井深增量（井段）： 下測點井深與上測點井深之差。以 ΔL 表示。
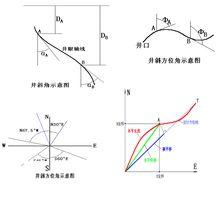測斜計算方法2. 井斜角( α )： 指井眼方向線與重力線之間的夾角。單位為度(°)。
井眼方向線： 過井眼軸線上某測點作井眼軸線的切線，該切線向井眼前進方向延伸的部分稱為井眼方向線。
井斜角增量( Δα )： 下測點井斜角與上測點井斜角之差。 Δα = α － α
3. 井斜方位角 φ 在水平投影圖上，以正北方位線為始邊，順時針方向旋轉到井眼方位線上所轉過的角度。
井眼方位線（井斜方位線）： 某測點處的井眼方向線在水平面上的投影。
井斜方位角增量 Δφ ： 上下測點的井斜方位角之差。 Δφ =φ －φ
井斜方位角的變化範圍：0～360° 。
4垂直深度 D （垂深）： 軌跡上某點至井口所在水平面的距離。垂深增量稱為垂增（ ΔD ）。
5. 水平投影長度 Lp （水平長度、平長）： 井眼軌跡上某點至井口的長度在水平面上的投影，即井深在水平面上的投影長度。水平長度的增量稱為平增（ ΔL ）。
6. 水平位移 S （平移）： 軌跡上某點至井口所在鉛垂線的距離（或：在水平投影面上，軌跡上某點至井口的距離）。
7.平移方位線 ：在水平投影面上，井口至軌跡上某點的連線。
8.我國將完鑽時的水平位移稱為 閉合距 。
9.平移方位角θ ： 平移方位線所在的方位角。
10. N坐標和E坐標： 南北坐標軸，以正北方向為正；
東西坐標軸，以正東方向為正。
11. 視平移V： 水平位移在 設計方位線 上的投影長度。
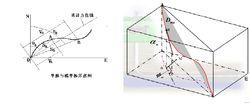測斜計算方法