基礎知識
整序的定義
整序源於英文sorting一詞,是對給定的一組數字或字元按照一定規則整理次序。整序又分為內部整序和外部整序。所謂的內部整序是指要整序的元素全部放在記憶體;所謂的外部整序是指要整序的元素存放在外存。
整序問題
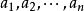 整序集法
整序集法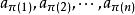 整序集法
整序集法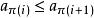 整序集法
整序集法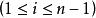 整序集法
整序集法整序問題定義為:給定一些全序(常用≤表示)集中抽出來的元素序列 ,找出一個置換π,它把給定的序列映射到一個非遞減序列 ,即, , 。
1.穩定的整序方法
在給定的n個元素序列整序時,若其中有幾個元素相同,上述定義的π不唯一。選擇一種π,使滿足:
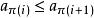 整序集法
整序集法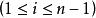 整序集法
整序集法(1) , ;
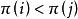 整序集法
整序集法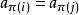 整序集法
整序集法(2)如果在已整序序列中 且 ,則必有i<j。
能夠產生這種唯一置換的π的整序方法稱為穩定的。
2.算法是原地的
一個對n個元素進行整序的算法,除了使用各別存儲單元或指針外,不用額外的存儲空間,則該算法稱為是原地的。
發展過程
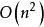 整序集法
整序集法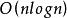 整序集法
整序集法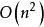 整序集法
整序集法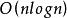 整序集法
整序集法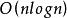 整序集法
整序集法雖然,第一個整序的電腦程式是由Von.Neumann寫於1946年,並在第一台計算機上運行,但是真正開始研究整序算法是20世紀50年代的事。最簡單的直觀的整序算法是選擇整序、冒泡整序和插入整序,但是它們的運行時間都是 。為了提高整序速度,人們不斷改進上述算法。1954年,D.L.Shell提出了縮小增量法,這是對插入整序的有效改進。1962年,O.A.R.Hoare提出了快速整序方法,它的平均時間複雜度是 ,而最壞情況下運行時間仍是 。1964年,由J.Williams首先提出而經Floyd改進的堆整序算法是一個既在平均情況下,又在最壞情況下,都是 的有效算法。這期間,人們還提出了一些別的整序算法,如歸併整序,基數整序等一些較成熟的算法。並且,在這期間,人們也認識到了比較整序的下界是 。到了70年代,整序方法的改進就更加精細了,Singeton在1969年,Frazer和Mokellar在1970年提出了對快速整序的改進。Blum,Floyd,Prattle,Rivest和Tarjan給出了O(n)時間的求順序統計量的算法。隨後,Floyd和Rivest又在1973年對此作了改進。
穩定的整序算法是Horvath在1974年提出的。大多數簡單算法是穩定的,而多數知名算法是不穩定的。1973年,Knuth在它的名著“the art of compter programming”第三卷中,對整序算法做了全面總結,使整序算法更系統,更完善。
1980年,Kunth的學生,Sedgewick在它的博士論文“Quick Sort”中,對快速整序作了全面、精細的分析,它的分析是對一個計算機算法進行數學分析的典範。
各種整序算法
選擇整序
1.地位:選擇整序是最簡單的整序算法之一,這個算法適宜於小型檔案。
2.基本思想:發現最小元素並放入第一個位置,然後找出次小元素放在第二個位置,這樣一直找下去,直至整個數組整隊好,將該方法稱為選擇整序。
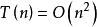 整序集法
整序集法3.算法分析:該算法的時間複雜度 。
插入整序
1.地位:插入整序是與選擇整序同樣簡單,但更為方便的是插入整序。
2.基本思想:類似於人們通常玩紙牌的方法,將它插入適當的位置,使它們保持大小順序,也就是說,將考慮的元素插入適當位置後將比其它的元素右移一個位置。
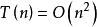 整序集法
整序集法3.算法分析:該算法的時間複雜度 。
冒泡整序
1.地位:冒泡整序是最簡單的整序算法之一。
2.基本思想:在整序的過程中,每次僅進行相鄰兩元素的比較,它不像選擇整序那樣一個較小元素一下子就放在頂部,而是每次向上移動一步,緩緩上升到頂部,活像一個氣泡從水底向上運動一樣。
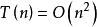 整序集法
整序集法3.算法分析:該算法的時間複雜度 。
歇爾整序
1.地位:歇爾整序是插入整序的推廣。
2.基本思想:先比較相距比較遠的元素,然後將比較的距離逐漸縮小,直至為1。
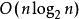 整序集法
整序集法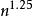 整序集法
整序集法3.算法分析:該算法的時間複雜度至今不甚明了,有兩個猜想:一個是 ,另一個是 。
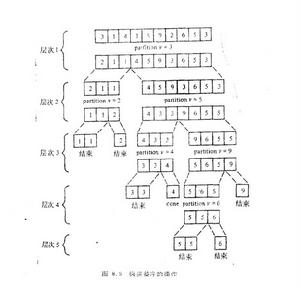
快速整序
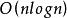 整序集法
整序集法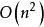 整序集法
整序集法至今,我們只考慮整序算法在最壞的情況下的行為。對很多套用來說,一個算法的時間複雜度的更現實的測度是平均複雜度。套用最廣泛的快速整序算法就是一個平均複雜度為 的有效算法,它是C.A.R.Hoare在1962年發明的。該算法可以寫成相當短的遞歸算法,但是,要把它寫成非遞歸算法,則它的程式就變得相當複雜;另外在最壞情況下,它的時間複雜度仍然是 ,而且是不穩定的。
基本思想:分而治之,把檔案分割成兩部分,然後獨立地對這兩個部分進行整序,實際的額分割點依賴於檔案的具體情況。
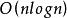 整序集法
整序集法算法分析:該算法的平均時間複雜度為 。
堆整序
1.堆的定義。
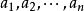 整序集法
整序集法堆是一種數據結構,它是用二叉樹的一個結點來表示集合{ }的一個元素,且滿足:
(1)二叉樹每片葉的深度是d或d-1(d是二叉樹高度);
(2)最底層葉子儘可能向左排;
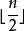 整序集法
整序集法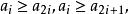 整序集法
整序集法(3)將1,2,…,n這n個數按從上到下,從左到右的次序賦給二叉樹各結點,對i=1,2,…, ,有: 其中,1≤i≤n。
2.堆的性質。
(1)從任一結點到葉子的通路上元素排列是有序的;
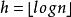 整序集法
整序集法(2)n個結點的堆,其高 ;
(3)n個結點的堆,對任一結點i,(1≤i≤n),有:
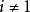 整序集法
整序集法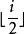 整序集法
整序集法①如果 ,則i的父親是 ,如果i=1,則i是根,無父親;
②如果2i=n,則i有一個兒子,它是2i;如果2i>n,則i無兒子。如果2i<n,則i有兩個兒子,左兒子2i和右 兒子2i+1。
基於上述性質,用一個一維數組來存貯堆是理想的。
3.堆整序
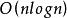 整序集法
整序集法(1)堆整序不用額外的存貯空間,就能在 時間內整序n個任意排列的元素。
(2)基本思想:將待整序數組A建成堆,則A(1)是最大元素,將其與A(n)交換,再重建A(1),…,A(n-1)稱為堆,再交換A(1)和A(n-1)…,這樣一直下去,直至重建堆的元素只剩A(1),此時A(1),…,A(n)便是從小到大排列了。
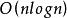 整序集法
整序集法(3)時間複雜度:堆整序的時間複雜度是 。