 圖片
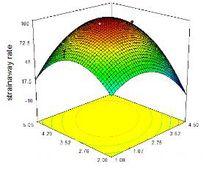
圖片效應面最佳化法主要考察自變數對效應的作用並對其進行最佳化。自變數必所考察的因素為自變數, 用x 1, x 2, ⋯, x k 表示;考察指標又稱結果或效應(respon se) , 為因變數, 用y 表示。須連續且可被實驗者準確控制。效應與考察因素之間的關係可用函式y =f (x 1, x 2, ⋯, x k ) + E表示(E為偶然誤差) , 該函式所代表的空間曲面稱為效應面。在實際操作中, 常用一近似函式y = f ′(x 1, x 2, ⋯, x k ) + E估計函式f , f ′所代表的空間曲面為模擬效應面, 也是最佳化法實際操作效應面。當有兩個考察因素時, 效應對考察因素的效應面可用三維效應面圖(或稱因變數面圖) 或二維等高線圖表示。從效應面上可以直觀地找到自變數取不同值時的效應值, 反過來在效應面上選取一定效應值亦可以找出相對應的自變數取值, 即在效應面上選定較佳效應值範圍後可對應求出較佳實驗條件。適用於效應面最佳化法的實驗設計稱效應面設計( respon se su rface design)。簡單地說, 效應面最佳化法就是通過描繪效應對考察因素的效應面, 從效應面上選擇較佳的效應區,從而回推出自變數取值範圍即最佳實驗條件的最佳化法。使用起來直觀、方便、效果較好。函式f 不可能用數學模型表述, 效應對因素的真實效應面只是假想的。但可以用某一數學模型f ′近似地模擬函式f ,依據該模型可以描繪效應面, 從而優選條件。數學模型f ′與f 的近似程度直接關係到效應面的近似程度與優選條件的準確度。RSM 最佳化過程包括: (1) 選擇可靠的實驗設計以適應線性或非線性模型擬合;(2) 建立效應與因素之間的數學關係式, 並通過統計學檢驗確保模型的可信度; (3) 優選最佳工藝條件。效應與因素之間的關係可能是線性的, 也可能是非線性的, 表現在效應面上, 線性的為平面, 非線性的為曲面。在整個考察範圍內, 在距離較佳區域較遠的地方接近線性, 愈接近較佳區, 面的彎曲度就越大,即在較佳區, 非線性關係居多。模型擬合優度用方差分析判別。根據模型可採用解方程求極值或限定效應範圍求解因素水平區間的辦法獲得較佳工藝條件。但最為簡單直觀的方法為描繪效應面, 從效應面上直接讀取較佳工藝條件。
