基本介紹
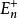 多面體擬陣
多面體擬陣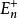 多面體擬陣
多面體擬陣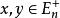 多面體擬陣
多面體擬陣 多面體擬陣
多面體擬陣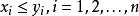 多面體擬陣
多面體擬陣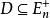 多面體擬陣
多面體擬陣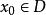 多面體擬陣
多面體擬陣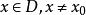 多面體擬陣
多面體擬陣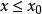 多面體擬陣
多面體擬陣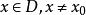 多面體擬陣
多面體擬陣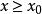 多面體擬陣
多面體擬陣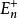 多面體擬陣
多面體擬陣設 為n維歐氏空間的那個非負象限,在 上定義一個偏序:對於 , 表示 ,設 ,若 具有這樣的性質:不存在 ,使得 ,則稱x為偏序D上的一個極小元,若不存在 ,使得 ,則x為D上的一個極大元,在 上的一個有界多面體擬陣就是這樣的一個多面體M,它具有性質:
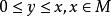 多面體擬陣
多面體擬陣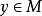 多面體擬陣
多面體擬陣1.若 ,則 ;
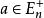 多面體擬陣
多面體擬陣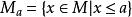 多面體擬陣
多面體擬陣2.對任何 ,集合 的所有極大元的分量和均相同,並且,這個和稱為a的秩。
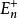 多面體擬陣
多面體擬陣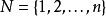 多面體擬陣
多面體擬陣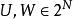 多面體擬陣
多面體擬陣在 上所定義的秩確定一個多面體擬陣的秩函式,在 的所有子集形成的簇2 上定義的函式ρ,若對任何 均有
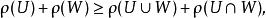 多面體擬陣
多面體擬陣則稱ρ為次模的,若上面的不等式是反向的,則稱ρ為上模的 。
有界多面體擬陣
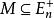 多面體擬陣
多面體擬陣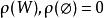 多面體擬陣
多面體擬陣一個多面體 是 有界多面體擬陣,若且唯若在2 上存在一個非降的次模函式 ,使得
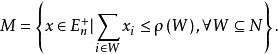 多面體擬陣
多面體擬陣無界多面體擬陣
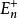 多面體擬陣
多面體擬陣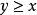 多面體擬陣
多面體擬陣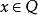 多面體擬陣
多面體擬陣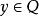 多面體擬陣
多面體擬陣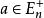 多面體擬陣
多面體擬陣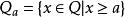 多面體擬陣
多面體擬陣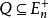 多面體擬陣
多面體擬陣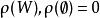 多面體擬陣
多面體擬陣在 上的一個無界多面體擬陣就是這樣的一個多面形Q,使它具有性質:若 ,和,則;對任何 ,在 中的每個極小元的分量和都相同,一個多面形 是一個 無界多面體擬陣,若且唯若存在2 上的一個上模函式 ,使得
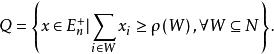 多面體擬陣
多面體擬陣多面體擬陣的序陣
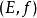 多面體擬陣
多面體擬陣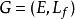 多面體擬陣
多面體擬陣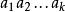 多面體擬陣
多面體擬陣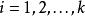 多面體擬陣
多面體擬陣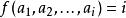 多面體擬陣
多面體擬陣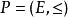 多面體擬陣
多面體擬陣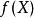 多面體擬陣
多面體擬陣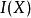 多面體擬陣
多面體擬陣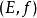 多面體擬陣
多面體擬陣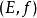 多面體擬陣
多面體擬陣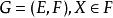 多面體擬陣
多面體擬陣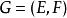 多面體擬陣
多面體擬陣多面體擬陣的序陣(polymatroid greedoid)是一種組合構形,它是由多面體擬陣派生的序陣,這裡f為符合要求的次模函式,序串為序陣G的可行詞,若且唯若對於任意的,均有。例如,在偏序集上,對於E的任意子集X,設表示由X產生的理想包含元素的個數,此時為一多面體擬陣,於是,可由派生序陣,記為若且唯若X為P上的一個理想,稱為偏序集序陣,或時間表序陣 。
相關介紹
擬陣多面體是一種組合構形,它是由擬陣M=(E,I)的所有獨立集的關聯向量生成的多面體P。
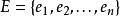 多面體擬陣
多面體擬陣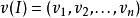 多面體擬陣
多面體擬陣記 ,獨立集I的關聯向量 ,當I包含元素e時,v=1,否則v=0,擬陣多面體的優越性在於,它可以藉助擬陣的秩函式r而表示為約束不等式的形式I(E,r):對於E的任意子集F,有
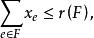 多面體擬陣
多面體擬陣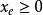 多面體擬陣
多面體擬陣且對於E的任意元素e,有 ,擬陣多面體P的頂點均為整值點,這樣建立在擬陣上的最佳化問題就可以歸結為不考慮其解是否取整數值的一般線性規劃問題,從而為擬陣上的最佳化問題開闢了一個新的領域,例如,下圖G上的圖擬陣M(G),其多面體由下述不等式決定 :
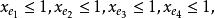 多面體擬陣
多面體擬陣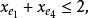 多面體擬陣
多面體擬陣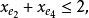 多面體擬陣
多面體擬陣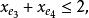 多面體擬陣
多面體擬陣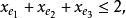 多面體擬陣
多面體擬陣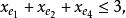 多面體擬陣
多面體擬陣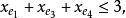 多面體擬陣
多面體擬陣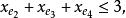 多面體擬陣
多面體擬陣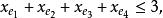 多面體擬陣
多面體擬陣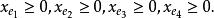 多面體擬陣
多面體擬陣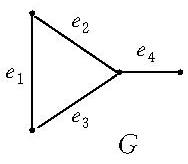 圖1
圖1在以約束不等式表示的擬陣多面體裡,若以G的滿足下述條件的一般整值次模函式f取代擬陣的秩函式:
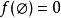 多面體擬陣
多面體擬陣1. ;
2.對於E的任意子集A,B,若A⊆B則:
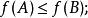 多面體擬陣
多面體擬陣3.對於E的任意子集A和B,有
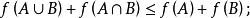 多面體擬陣
多面體擬陣則不等式組I(E,f)決定的多面體,其頂點仍對應於某個擬陣的獨立集,由I(E,f)決定的擬陣稱為 多面體擬陣 。