Morgan’s Law
一.摩根定律
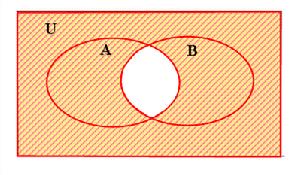摩根定律——交集的補集韋恩圖Cu(A∩B)=CuA∪CuB,
稱為摩根定律.又叫反演律.
摩根定律用文字語言可以簡單的敘述為:
兩個集合的交集的補集等於它們各自補集的並集;
兩個集合的並集的補集等於它們各自補集的交集.
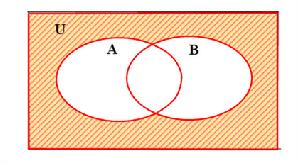摩根定律——並集的補集韋恩圖Cu(∪Ai)=∩CuAi, i=1,2,3,…,n.
Cu(∩Ai)=∪CuAi, i=1,2,3,…,n.
稱為摩根定律.又叫反演律.
二.摩根定律的套用
摩根定律實現了集合運算的匯集,轉化,簡化以及與邏輯命題的聯繫.
1.集集合的三大運算於一身,並可以使它們互相轉化,尤其是交運算與並運算的轉化.
2.可以把“補補交”三次運算，化簡為“並補”兩種運算等。
3.在邏輯中，複合命題“p且q”，“p或q”的否定完全遵循摩根定律。
(1)非“p且q”非p或非q.理解為非“p且q”是對“p且q”的否定.即不是p,q都真,而是p,q至少一個假.
(２) 非“p或q”非p且非q. 理解為非“p或q”是對“p或q”的否定.即不是p,q都至少一個真,而是p,q都假.
三.套用舉例
U={x | x=3n ，x<30,n∈N*}, CuA∩B={6.15}, A∩CuB={3.21} , CuA∩CuB={9，18，24} .求集合A ∩B.
範例解答
如圖.
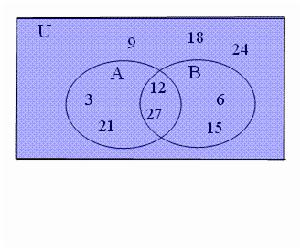韋恩圖CuA∩CuB={9，18，24}，
由摩根定律
Cu(A∪B)= {9，18，24}，
∴A∪B={3,6,12,15,21,27}。
又CuA∩B={6.15}，
A∩CuB={3.21}，
∴A∩B={12,27}。
四.德·摩根簡介
摘自<互動百科>詞條”德·摩根”.
德·摩根 Augustus De Morgan (1806～1871)
德·摩根
19世紀英國數學家、邏輯學家。生於印度，出生後剛 7個月就回到英國。卒於倫敦。他在少年時代就對數學發生濃厚的興趣，1823年考入劍橋大學三一學院，1827年畢業。1828年後在倫敦的大學學院任數學教授多年。他曾任倫敦數學學會第一屆會長。
德·摩根對19世紀數學的發展作出了貢獻。他於1838年提出以“數學歸納法”的概念描述以往數學家們曾經使用的證明定理的方法。1842年，他發表了《微積分演算》一文，詳盡討論微積分基本原理和極限定義，並討論了無窮序列及確定序列收斂的新規則。他曾從事當時稱為“形式代數”的研究，其成果有助於對複數的性質給出一個完全的幾何解釋。
德·摩根的主要成就在邏輯方面，主要邏輯著作是《形式邏輯》（1847）。他在邏輯史上首先提出“論域”的概念，第一次明確用公式表達合取和析取的關係，現代邏輯稱之為德·摩根律。
他還最先提出了關於“大多數”的推理。他對邏輯的最主要貢獻在於開拓了形式邏輯的新領域，建立了關係邏輯，有的學者稱他為“關係邏輯之父”。他對關係的種類和性質作了研究，並使用了一些他自己所創造的符號。
德·摩根提出了一些重要的關係邏輯規律，以及一些推理形式等。
五.參考資料
１.數學奧林匹克訓練教程.
２.高中數學基礎知識全書.
３.數學手冊.
