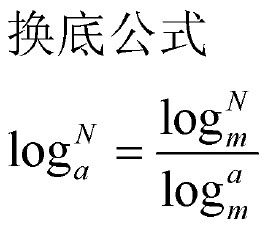換底公式

換底公式是一個比較重要的公式，在很多對數的計算中都要使用，也是高中數學的重點。另有兩個推論如下：log a(b)表示以a為底的b的對數。換底公式就是log(a)(b)=log(c)(b)/log(c)(a)(a,c均大於零且不等於1）。

基本信息

• 中文名：換底公式
• 英文名：base changing formula for lograithms

• 適用學科：數學、計算機
• 適用範圍：對數的計算，高中數學
• 公式成立條件：a,c均大於零且不等於1
• 推論個數：2

形式

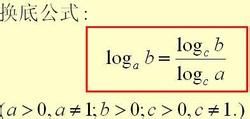換底公式

換底公式是一個比較重要的公式，在很多對數的計算中都要使用，也是高中數學的重點。另有兩個推論。
loga(b)表示以a為底的b的對數。
換底公式就是
log(a)(b)=log(c)(b)/log(c)(a)(a,c均大於零且不等於1）

推導過程

若有對數log（a）（b）設a=n^x,b=n^y(n>0,且n不為1)如：log（10）（5）=log（5）（5）/log（5）（10）
則 log（a）（b）=log（n^x）(n^y)
根據對數的基本公式
log(a）(M^n)=nloga(M)和 基本公式log(a^n)M=1/n×log(a) M
易得
log(n^x)(n^y)=y/x
由 a=n^x,b=n^y可得 x=log(n)(a),y=log(n)(b)
則有：log(a)(b)=log(n^x)(n^y)=log(n)(b)/log(n)(a)
得證：log(a)(b)=log(n)(b)/log(n)(a)
例子：log(a)(c) * log(c)(a)=log(c)(c)/log(c)(a) *log(c)(a)=log(c)(c)=1

套用

數學對數

在數學對數運算中，通常是不同底的對數運算，這時就需要換底。.
通常在處理數學運算中，將一般底數轉換為以e為底（即In）的自然對數或者是轉換為以10為底（即lg）的常用對數，方便於我們運算；有時也通過用換底公式來證明或求解相關問題；
在計算器上計算對數時需要用到這個公式。例如，大多數計算器有[ln]和[log10]的按鈕，但卻沒有[log2]的。要計算log2(3)，你只有計算log10(3) / log10(2)（或 ln(3)/ln(2)，兩者結果一樣）；

工程技術

在工程技術中，換底公式也是經常用到的公式，
例如，在程式語言中，有些程式語言（例如C語言）沒有以a為底b為真數的對數函式；只有以常用對數10為底的對數或自然對數e為底的對數（即Ig、In）,此時就要用到換底公式來換成以e或者10為底的對數來表示出以a為底b為真數的對數表達式，從而來處理某些實際問題。