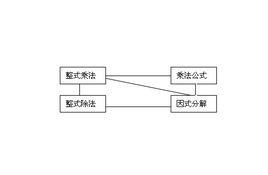
法則
具體方法:當各項係數都是整數時,公因式的係數應取各項係數的最大公約數;字母取各項的相同的字母,且各字母的指數取次數最低的;取相同的多項式,且多項式的次數取最低的。
如果多項式的第一項是負的,一般要提出“ -”號,使括弧內的第一項的係數成為正數。 提出“-”號時,多項式的各項都要變號。
 提公因式法
提公因式法例題:
顯然,提公因式法也是需要一定技巧的。
再看一道例題:(y-x)^2+y-x =(y-x)^2+(y-x)=(y-x+1)(y-x)
確定公因式的方法:
★確定公因式的一般步驟
(1)如果多項式的第一項係數是負數時,應把公因式的符號“-"提取。
(2)取多項式各項係數的最大公約數為公因數的係數。
(3)把多項式各項都含有的相同字母(或因式)的最低次冪的積作為公因式的因式。
上述步驟不是絕對的,當第一項是正數時步驟(1)可省略。
注意:
如果多項式的第一項是負的,一般要提出負號,使括弧內第一項係數是正的。防止學生出現諸如:
-9x^2+6xy= -3x(3x+2y)的錯誤。
口訣:找準公因式,一次要提淨;若搬全家走,留1把家守;提正不變號,提負就變號 。
解題步驟
提取公因式法是因式分解的一種基本方法。如果多項式的各項有公因式,可以把這個公因式提取出來作為多項式的一個因式,提取公因式後的式子放在括弧里,作為另一個因式。
提取公因式是乘法分配律的逆運算,其最簡形式為:ma+mb+mc=m(a+b+c) 。
提取公因式法分解因式的解題步驟是怎樣的?
利用提公因式法分解因式時,一般分兩步進行:
(1)提公因式。把各項中相同字母或因式的最低次冪的積作為公因式提出來;當係數為整數時,還要把它們的最大公約數也提出來,作為公因式的係數;當多項式首項符號為負時,還要提出負號 。
(2)用公因式分別去除多項式的每一項,把所得的商的代數和作為另一個因式,與公因式寫成積的形式。
由於題目形式千變萬化,解題時也不能生搬硬套。例如,有的需要先對題目適當整理變形;有的分解因式後多項式因式中有同類項的還要進行合併化簡;還有的提取公因式後能用其他方法繼續分解。