拿破崙三角

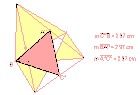
定義

在任意一個三角形的三條邊上分別向外做出三個等邊三角形,則這三個等邊三角形的中心也構成一個等邊三角形!!!

證明

證明：設三角形ABC對應邊外的正三角形的中心分別為D，E，F，
則：∠FAB=∠FBA=∠DBC=∠DCB=∠EAC=∠ECA=30
在多邊形AFBDCE中作一點G,使AG=AF,GE=DC,
連GF,GA,GE,
因△ABF,△BCD,△ACE均為底角等於30度的等腰三角形,
所以:△ABF∽△BCD∽△ACE
AF/AB=AE/AC=DC/BC
而AG=AF,GE=DC
所以,AG/AB=AE/AC=GE/BC,
△AGE∽△ABC
∠GAE=∠BAC,∠AGE=∠ABC
∠FAG=∠EAF-∠GAE=∠EAF-∠BAC=60
△AGF為等邊三角形
AG=AF, ∠AGF=60,
在△FBD和△FGE中，
FB=FG, BD=GE, ∠FBD=∠FGE
△FBD≌△FGE, (s.a.s)
FD=FE
同理可證:FD=DE
則 △DEF為等邊三角形 <證畢>