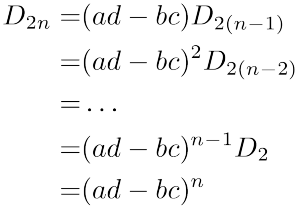拉普拉斯展開

在數學中，拉普拉斯展開（或稱拉普拉斯公式）是一個關於行列式的展開式。將一個n×n矩陣B的行列式進行拉普拉斯展開，即是將其表示成關於矩陣B的某一行（或某一列）的 n個元素的(n-1) × (n-1)餘子式的和。

基本信息

• 中文名：拉普拉斯展開

• 領域：數學
• 分類：關於行列式的展開式
• 備註：公式

簡介

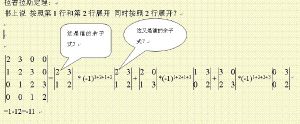拉普拉斯展開

行列式的拉普拉斯展開一般被簡稱為行列式按某一行（或按某一列）的展開。由於矩陣

有

行

列，它的拉普拉斯展開一共有2

種。拉普拉斯展開的推廣稱為拉普拉斯定理，是將一行的元素推廣為關於

行的一切子式。它們的每一項和對應的代數餘子式的乘積之和仍然是

的行列式。研究一些特定的展開可以減少對於矩陣

之行列式的計算，拉普拉斯公式也常用於一些抽象的推導中。

公式

設B = (bij)是一個n × n矩陣。B關於第i行第j列的餘子式Mij是指B中去掉第i行第j列後得到的n−1階子矩陣的行列式。有時可以簡稱為B的（i，j）餘子式。B的（i，j）代數餘子式：Cij是指B的（i，j）餘子式Mij與(−1)^(i+j)的乘積：Cij= (−1)^(i+j) Mij

拉普拉斯展開最初由范德蒙德給出，為如下公式：

對於任意i,j∈ {1, 2, ...,n}：|B| = bi1Ci1 +bi2Ci2 +... +binCin = b1jC1j +b2jC2j +... +bnjCnj