作者介紹
克萊姆(Cramer,Gabriel,瑞士數學家 1704-1752)克萊姆1704年7月31日生於日內瓦,早年在日內瓦讀書,1724 年起在日內瓦加爾文學院任教,1734年成為幾何學教授,1750年任哲學教授。他自 1727年進行為期兩年的旅行訪學。在巴塞爾與約翰.伯努利、歐拉等人學習交流,結為摯友。後又到英國、荷蘭、法國等地拜見許多數學名家,回國後在與他們的長期通信 中,加強了數學家之間的聯繫,為數學寶庫也留下大量有價值的文獻。他一生未婚,專心治學,平易近人且德高望重,先後當選為倫敦皇家學會、柏林研究院和法國、義大利等學會的成員。
主要著作是《代數曲線的分析引論》(1750),首先定義了正則、非正則、超越曲線和無理曲線等概念,第一次正式引入坐標系的縱軸(Y軸),然後討論曲線變換,並依據曲線方程的階數將曲線進行分類。為了確定經過5 個點的一般二次曲線的係數,套用了著名的“克萊姆法則”,即由線性方程組的係數確定方程組解的表達式。該法則於1729年由英國數學家馬克勞林得到,1748年發表,但克萊姆的優越符號使之流傳。
基本介紹
一般來說,用克萊姆法則求線性方程組的解時,計算量是比較大的。使用克萊姆法則求線性方程組的解的算
 克萊姆法則
克萊姆法則 法時間複雜度依賴於矩陣行列式的算法複雜度O(f(n)),其複雜度為O(n·f(n)),一般沒有計算價值,複雜度太高。. 對具體的數字線性方程組,當未知數較多時往往可用計算機來求解。用計算機求解線性方程組目前已經有了一整套成熟的方法。
概念
在引入克萊姆法則之前,先引入有關 n元線性方程組和有關矩陣、行列式的概念。含有 n個未知數的線性方程組稱為 n元線性方程組。
當其右端的常數項b,b,...,b不全為零時,線性方程組⑴稱為非齊次線性方程組。
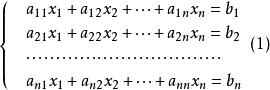 克拉默法則
克拉默法則  克拉默法則
克拉默法則  克拉默法則
克拉默法則 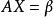 克拉默法則
克拉默法則 令
,其中A是線性方程組的係數矩陣,X是由未知數組成的列向量,是由常數項組成的列向量。線性方程組⑴的矩陣形式為。當常數項全為零時,線性方程組⑵稱為齊次線性方程組,即:
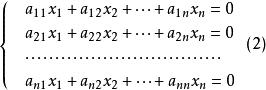 克拉默法則
克拉默法則 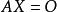 克拉默法則
克拉默法則 線性方程組(2)的矩陣形式為
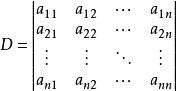 克拉默法則
克拉默法則 係數構成的行列式稱為該方程組的係數行列式D,即
定理
記法1:若線性方程組⑴的係數矩陣可逆(非奇異),即係數行列式 D≠0。有唯一解,其解為
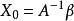 克拉默法則
克拉默法則 記法2:若線性方程組⑴的係數矩陣可逆(非奇異),即係數行列式 D≠0,則線性方程組⑴有唯一解,其解為
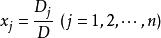 克拉默法則
克拉默法則 其中D是把D中第j列元素對應地換成常數項而其餘各列保持不變所得到的行列式。
記法1是將解寫成矩陣(列向量)形式,而記法2是將解分別寫成數字,本質相同。
證明
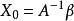 克拉默法則
克拉默法則 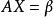 克拉默法則
克拉默法則 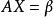 克拉默法則
克拉默法則 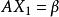 克拉默法則
克拉默法則 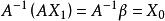 克拉默法則
克拉默法則 充分性:設A可逆,那么顯然是的一個解。又設X是其他不為X的解,即。兩邊同時左乘A 得
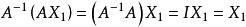 克拉默法則
克拉默法則 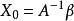 克拉默法則
克拉默法則 上面兩式矛盾,因為不存在其他不為X的解,故是的一個解。
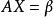 克拉默法則
克拉默法則 必要性:設的唯一解X如A不可逆,齊次線性組AX=O就有非零解Y,
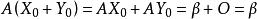 克拉默法則
克拉默法則 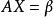 克拉默法則
克拉默法則 X0+Y0也是的一個解,矛盾,故不可逆,證畢。
推論
n元齊次線性方程組有非零解的充要條件是其係數行列式為零。等價地,方程組有唯一的零解的充要條件是係數矩陣的行列式不為零,其矩陣可逆。
法則總結
1. 克萊姆法則的重要理論價值:研究了方程組的係數與方程組解的存在性與唯一性關係;與其在計算方面的作用相比,克萊姆法則更具有重大的理論價值。
2.套用克萊姆法則判斷具有N個方程、N個未知數的線性方程組的解:
(1)當方程組的係數行列式不等於零時,則方程組有解,且具有唯一的解;
(2)如果方程組無解或者有兩個不同的解,那么方程組的係數行列式必定等於零
(3)克萊姆法則不僅僅適用於實數域,它在任何域上面都可以成立。
3.克萊姆法則的局限性:
(1)當方程組的方程個數與未知數的個數不一致時,或者當方程組係數的行列式等於零時,克萊姆法則失
效。
(2)運算量較大,求解一個N階線性方程組要計算N+1個N階行列式。
技術套用
克萊姆法則在解決微分幾何方面十分有用。
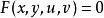 克拉默法則
克拉默法則 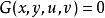 克拉默法則
克拉默法則 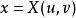 克拉默法則
克拉默法則 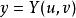 克拉默法則
克拉默法則 先考慮兩條等式和。因為u和v都是沒相關的變數,我們可定義和。
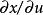 克拉默法則
克拉默法則 找出一條等式適合是克萊姆法則的簡單套用。
首先,我們要計算F、G、x和y的導數:
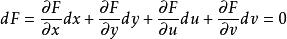 克拉默法則
克拉默法則 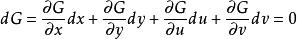 克拉默法則
克拉默法則 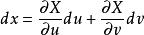 克拉默法則
克拉默法則 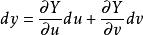 克拉默法則
克拉默法則 將dx和dy代入dF和dG,可得出:
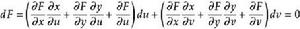 克拉默法則
克拉默法則 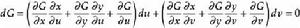 克拉默法則
克拉默法則 因為u和v都沒有關係,所以du和dv的係數都要等於0。所以等式中的係數可以被寫成:
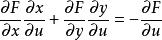 克拉默法則
克拉默法則 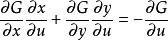 克拉默法則
克拉默法則 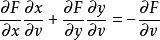 克拉默法則
克拉默法則 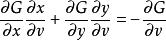 克拉默法則
克拉默法則 用克萊姆法則就可得到:
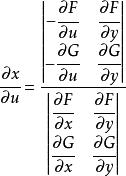 克拉默法則
克拉默法則 用兩個雅可比矩陣來表示的方程:
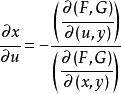 克拉默法則
克拉默法則 b
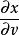 克拉默法則
克拉默法則 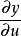 克拉默法則
克拉默法則 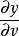 克拉默法則
克拉默法則 用類似的方法就可以找到、以及。
不確定的情況
當方程組沒有解時,稱為方程組不兼容或不一致,當存在多個解決方案時,稱為不確定性。對於線性方程,不確定的系統將具有無窮多的解(如果它在無限域上),因為解可以用一個或多個可以取任意值的參數來表示。
克拉默規則適用於係數行列式非零的情況。在2×2的情況下,如果係數行列式為零,則如果分子決定因子為非零,則系統不兼容,如果分子決定因素為零,則系統不兼容。
對於3×3或更高的系統,當係數行列式等於零時,唯一可以說的是,如果任何分子決定因素是非零的,那么系統必須是不兼容的。然而,將所有決定因素置零都不意味著系統是不確定的。 3×3系統x + y + z = 1,x + y + z = 2,x + y + z = 3的一個簡單的例子,其中所有決定因素消失(等於零)但系統仍然不兼容。

