應變張量
正文
連續介質力學中度量變形的幾何量。在直角坐標系中,未變形物體和已變形物體中線元的平方分別為:,
其中和
分別稱為柯西應變張量和格林應變張量或右柯西-格林張量。 這兩個張量都是對稱正定的。另外, 和
分別稱為芬格應變張量或左柯西-格林張量和皮奧拉應變張量。連續介質中兩相鄰粒子的ds2-dS2可以用來作為變形的度量。可以寫作:
,
式中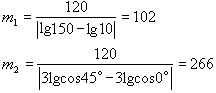
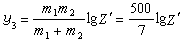

應變張量:是應變狀態的數學表示。數學上應變為二階張量,二維平面中需四個分量,三維空間中則需九個分量(三個線應變分量和六個剪應變分量)予以確定。
,
其中和
分別稱為柯西應變張量和格林應變張量或右柯西-格林張量。 這兩個張量都是對稱正定的。另外, 和
分別稱為芬格應變張量或左柯西-格林張量和皮奧拉應變張量。連續介質中兩相鄰粒子的ds2-dS2可以用來作為變形的度量。可以寫作:
,
式中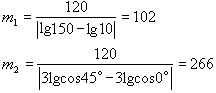
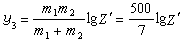
張量(tensor)理論是數學的一個分支學科,在力學中有重要套用。張量這一術語起源於力學,它最初是用來表示彈性介質中各點應力狀態的,後來張量理論發展成為...
物理名稱 背景知識 規定 定義 基本運算張量空間(tensor space)是多重線性代數的重要概念,定義是有張映射的一種向量空間。多重線性代數式代數學的一個重要分支。可以將它看做是線性代數的...
線性代數 因子化泛性質 張映射 多重線性代數 向量空間是物理學中場的一種。假如一個空間中的每一點的屬性都可以以一個張量來代表的話,那么這個場就是一個張量場。最常見的張量場有廣義相對論的應力能張量場(Stre...
套用 幾何式介紹理性力學中常用的一個張量。
正文 配圖 相關連線應力偏張量是塑性變形時物體內一點的應力張量的分量隨坐標變化而改變,但其應力張量不變數卻是固定不變的,因此應力張量不變數可以反映物體變形狀態的實質。
概述 相關詞條笛卡爾張量又叫做笛卡爾坐標系,是直角坐標系和斜角坐標系的統稱。相交於原點的兩條數軸,構成了平面仿射坐標系。如兩條數軸上的度量單位相等,則稱此仿射坐標係為...
概述 產生 相關詞條應變指適應時事變化、應付事態變化。
詞語相關 物理術語 圖書信息 相關典籍地震矩張量,地震學術語,地震矩的張量表示形式,它取決於震源的方向和強度。用地震矩張量可將震源表示為膨脹源、剪下位錯源和補償線性向量偶極三部分之和。
機制原理 測定方法 震源參數 相關知識 相關詞條