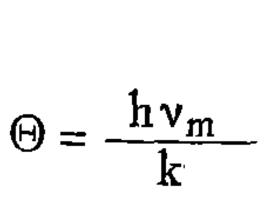定義
原子在金屬晶體中的熱運動， 對於闡明金屬的比熱， 熱膨脹， 相變， 範性形變等方面起著重要的作用。所謂原子的熱運動是指原子在絕對零度以上時， 由於溫度的影響， 使原子在平衡位置作一定的振動， 這種振動可以用晶體物質的所謂德拜特徵溫度Θ來加以描述：
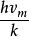德拜特徵溫度Θ=
式中h 為普朗克常數，
k 為玻耳茲曼常數；
v為在某一溫度下固體中核子彈性振動的最大頻率。
特徵溫度Θ，不但與許多參量有著定量的關係，而且還能論證物質內在的本質。
測定原理
根據比熱理論的計算， 晶體中某一晶面(hkl) ， 由於原子熱振動使得X 射線衍射束強度I和沒有( 理想化) 熱振動時X 射線衍射束強度I之比為
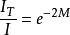德拜特徵溫度(1)
式中e 稱為溫度因素，2M與其他物理量的關係為：
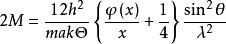德拜特徵溫度(2)
德拜特徵溫度
德拜特徵溫度式中h為普朗克常數， h =6.62510 爾格秒，ma為原子的質量，k 為玻爾茲曼常數k=1.3805×10 爾格/度，Θ為德拜溫度，T 為絕對溫度， θ為半衍射角，λ為所用射線波長，由所謂零點能量而來的，φ（x）稱為德拜函式，可由國際X 射線晶體學表中查出。
今若在T1和T2 兩個溫度下拍攝同一試樣中某一晶面(hkl)的衍射譜線， 其強度分別為IT1和IT2， 則根據( 1 ) 式可得：
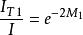德拜特徵溫度(3)
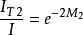德拜特徵溫度(4)
兩式兩邊取ln後相減，得：
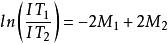德拜特徵溫度將（2）式代入整理後得：
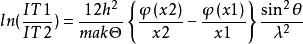德拜特徵溫度
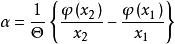德拜特徵溫度令：
則式（6）可寫成：
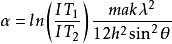德拜特徵溫度特徵溫度的性質
1、由( 1 )、( 2 ) 式可知， 當Θ減小時， M 的數量增加， 因而衍射強度下降，所以說x 射線衍射強度下降效應， 相當於特徵溫度的減小。
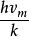德拜特徵溫度2、由Θ=可知：Θ的量綱是溫度，它隨著自然振動頻率v而變(v 是v的最大值) 。
3、Θ愈大時，原子難以離開平衡位置。
4、由( 2 ) 式可知， M 隨sinθ/λ和溫度增加而增加， 當λ， T 一定時， 晶面指數(hkl) 大， M 大， 這就是說晶體密勒指數大的衍射譜線比密勒指數小的衍射譜線強度下降明顯， 這點暗示我們， 在測定Θ溫度的工作中， 採用( h kl ) 大的譜線是比較好的。
5、(2)是由同種原子構成的簡單立方晶體推導出來的， 但是對於其他由單一原子組成的密排結構也有較好的適應性， 例如Be ， Mg ， Ca 等； 不是單一原子的非立方晶體和立方晶體， 如Nacl ， Kcl ， KBr ， 金剛石等， 都用此法進行了測定， 得到滿意的結果 。
6、特徵溫度的非均勻性：
如果晶體結構內包含著不止一種原子， 而各原子的振動模式又各個不同， 則這個晶體的溫度因數是非均勻性的， 因此， 這個晶體中原子的特徵溫度也是非均勻性的。
7、特徵溫度的各向異性。
