正文
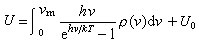德拜模型德拜模型把原子排列成晶體點陣的固體看作是一個連續彈性媒質，原子間的作用力遵從胡克定律，組成固體的 N個原子在三維空間中集體振動的效果相當於3N個不同頻率的獨立線性振子的集合。每一個獨立諧振子的振動是一種簡正振動模式，彈性媒質的一種簡正振動模式是具有一定頻率、波長和傳播方向的彈性波。彈性固體能夠以不同的速度傳播縱、橫兩種波。對於每一個振動頻率，縱波只有在傳播方向的一種振動，橫波有兩種垂直於傳播方向的振動（兩個偏振），共三個振動模式。為把固體看作是連續的彈性媒質，德拜模型只考慮那些頻率非常低（近似取為零）直到極限頻率vm範圍內的振動模式。由於N的數目很大,3N種振動頻率可看作是連續分布在零到vm區間內，則3N個不同頻率的獨立諧振子的總能量就由分立的求和變為積分
，
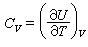德拜模型Uo是同溫度無關的常數, ρ(v)稱頻率分布函式。用熱力學關係
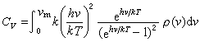德拜模型,由點陣振動導致的固體的定容熱容是
。
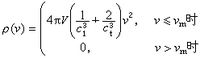德拜模型ρ(v)的形式是
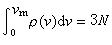德拜模型其中V是固體的體積,с1、сt分別是固體中縱波和橫波的傳播速度。由條件
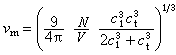德拜模型可得到德拜最大頻率是
，
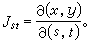德拜模型而ρ(v)就可寫成
德拜模型。令x=hv/kT, 便導出了固體的摩爾熱容
，
其中嘷D＝hvm/k稱德拜溫度。
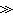德拜模型上式在T
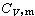德拜模型嘷D時導出
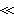德拜模型＝3R(R是摩爾氣體常數),就是經典結果；當T
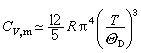德拜模型嘷D時，可得
，
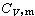德拜模型隨著T→0,
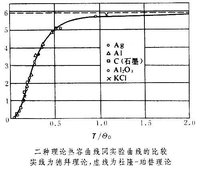
德拜模型按T趨於零。對中間溫度區域,則需用數值計算求積分值。對於一些簡單結構的固體，其熱容的理論曲線同實驗結果的比較見圖。圖中同時畫出了杜隆-珀替定律的曲線（圖中虛線）。可見，德拜模型導出的熱容公式同實驗符合得很好。
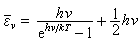德拜模型根據量子論，德拜所考慮的彈性波的簡正振動能量也是量子化的，是最小能量hv的倍數。彈性波的這一最小能量稱為聲子,它是固體原子系統的集體激發模式,可看作是在點陣中傳播的具有一定能量和運動方向的準粒子。把彈性聲波場當作聲子系統處理後，再把普朗克公式運用到固體點陣振動上,頻率為v的振子振動的平均能量就是
，那么3N個不同頻率的獨立諧振子的總能量是各振子平均能量的和。
德拜模型不能用於以下幾種情況：①較複雜的分子，特別是高度各嚮導性晶體，前述的頻率分布函式不適用時；②波長同點陣間距離可比擬，破壞了連續媒質的構想時；③極低溫度下，電子參與對熱容貢獻並起主要作用時（見電子比熱容）。
德拜的推導
實際上，德拜用不同和更加簡單的方法推出了這個方程。利用連續介質的固體力學，他發現頻率小於某個特定值的振動狀態的數目趨近於：
n \sim {1 \over 3} \nu^3 V F\,,
其中V是體積，F是一個因子，他從彈性係數和密度計算。把這與溫度T的量子諧振子的期望能量（已經由愛因斯坦在他的模型中使用）結合，便給出能量：
U = \int_0^\infty \,{h\nu^3 V F\over e^{h\nu/kT}-1}\, d\nu\,,
如果振動頻率趨於無窮大。這個形式給出了T4的表現，它在低溫時是正確的。但德拜意識到N個原子不可能有超過3N個振動狀態。他假設在原子固體中，振動狀態的頻譜將繼續遵循以上的規則，到一個最大的頻率νm為止，使得總的狀態數目為3N：
3N = {1 \over 3} \nu_m^3 V F \,.
德拜知道這個假設不是真正正確的（較高的頻率比假設要更加密集），但它保證了高溫時的正確表現（杜隆-珀蒂定律）。於是，能量由以下給出：
U = \int_0^{\nu_m} \,{h\nu^3 V F\over e^{h\nu/kT}-1}\, d\nu\,,
= V F kT (kT/h)^3 \int_0^{T_D/T} \,{x^3 \over e^x-1}\, dx\,,
其中TD是hνm / k。
= 9 N k T (T/T_D)^3 \int_0^{T_D/T} \,{x^3 \over e^x-1}\, dx\,,
= 3 N k T D_3(T_D/T)\,,
其中D3是一個函式，後來命名為三階德拜函式。
