簡介
 &amp
&amp後驗機率是指在得到“結果”的信息後重新修正的機率,是“執果尋因”問題中的"果"。先驗機率與後驗機率有不可分割的聯繫,後驗機率的計算要以先驗機率為基礎 。
事情還沒有發生,要求這件事情發生的可能性的大小,是先驗機率。事情已經發生,要求這件事情發生的原因是由某個因素引起的可能性的大小,是後驗機率。
先驗機率不是根據有關自然狀態的全部資料測定的,而只是利用現有的材料(主要是歷史資料)計算的;後驗機率使用了有關自然狀態更加全面的資料,既有先驗機率資料,也有補充資料;
先驗機率的計算比較簡單,沒有使用貝葉斯公式;而後驗機率的計算,要使用貝葉斯公式,而且在利用樣本資料計算邏輯機率時,還要使用理論機率分布,需要更多的數理統計知識。
實例
假設一個學校里有60%男生和40%女生。女生穿褲子的人數和穿裙子的人數相等,所有男生穿褲子。一個人在遠處隨機看到了一個穿褲子的學生。那么這個學生是女生的機率是多少?
使用貝葉斯定理,事件A是看到女生,事件B是看到一個穿褲子的學生。我們所要計算的是P(A|B)。
P(A)是忽略其它因素,看到女生的機率,在這裡是40%
P(A')是忽略其它因素,看到不是女生(即看到男生)的機率,在這裡是60%
P(B|A)是女生穿褲子的機率,在這裡是50%
P(B|A')是男生穿褲子的機率,在這裡是100%
P(B)是忽略其它因素,學生穿褲子的機率,P( B) = P( B| A)P( A) + P( B| A')P( A'),在這裡是0.5×0.4 + 1×0.6 = 0.8。
根據貝葉斯定理,我們計算出後驗機率P(A|B)
P(A|B)=P(B|A)*P(A)/P(B)=0.25
可見,後驗機率實際上就是條件機率。
抽樣方法
在統計學和金融經濟學中,隨機變數X的機率分布為 f(x|θ),先驗機率分布為 f(θ),根據貝葉斯定理,後驗機率分布為f(θ|x):
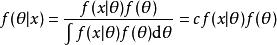 後驗機率
後驗機率式中,歸一化常數c的積分是高維積分,是很難進行數值計算的,因此歸一化常數c可以認為是未知的,所以後驗機率分布是不完全已知機率分布。對於不完全已知機率分布,直接抽樣方法不適用,應採用間接抽樣方法,如馬爾科夫鏈蒙特卡洛方法。
解釋
1、當根據經驗及有關材料推測出主觀機率後,對其是否準確沒有充分把握時,可採用機率論中的貝葉斯公式進行修正,修正前的機率稱為先驗機率,修正後的機率稱為後驗機率,利用後驗機率再進行風險分析。
2、信息技術革命加快了人類邁向信息社會實際情況的進程,世界信息服務業正在成為最強勁的實質上,它是以新的信息做為條件的條件概經濟成長點。
3、P{H0|x}是給定觀測值x條件下H0齣現的機率,統稱為後驗機率。根據貝葉斯公式,後驗機率可表示為P{H0|x}=P(H0)P{x|H0}/P(x),P{H1|x}=P(H1)P{x|H1}/P(x)。式中,P(x)為x的機率密度。
4、也就是獲得條件機率P(ωωt-k),這個機率常常稱為後驗機率。利用後驗機率進行系統的狀態決策無疑是更加合理的方法,因為它充分利用了先驗知識和觀測到歷史時間變數的信息。
5、這個機率稱為後驗機率,根據貝葉斯規則計算如下:P[^ωΦ(t)]=maxωP[Φ(t)ω]P(ω)P[Φ(t)],這裡的條件機率P[Φ(t)ω]是比較故障模型和輸入模式之間符合程度的結果。
例子
舉一個簡單的例子:一口袋裡有3隻紅球、2隻白球,採用不放回方式摸取,求:
⑴ 第一次摸到紅球(記作A)的機率;
⑵ 第二次摸到紅球(記作B)的機率;
⑶ 已知第二次摸到了紅球,求第一次摸到的是紅球的機率。
解:
⑴ P(A)=3/5,這就是驗前機率;
⑵ P(B)=P(A)P(B|A)+P(A逆)P(B|A逆)=3/5
⑶ P(A|B)=P(A)P(B|A)/P(B)=1/2,這就是後驗機率。