簡介
以下內容來自部分維基
經驗機率(Empirical probability)或稱實驗機率(experimental probability),也稱為相對頻率(Relative frequency),是指特定的事件發生的次數占總體實驗樣本的比率 。經驗機率並不是一個理論取樣範疇,而是通過實際實驗取得的。大致上來說,經驗機率是從實驗和實際觀測中估算的機率。
在取樣空間中,給定一個事件A,事件A的經驗機率=事件A發生次數/全部觀測次數。
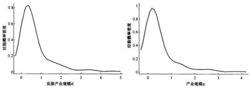 經驗機率
經驗機率在統計學上講,經驗機率是一個被估算的機率值,或稱為機率的估算值。在簡單情況下,這樣一個試驗的結果只決定某特定事件是否發生。此時,可以用二項分布法進行建模,然後用最大似然法進行經驗機率的估算。同樣,如果已對機率的先驗值做了具體的假設,則可以用貝葉斯法進行估算。如果一個試驗包含有更多信息,我們可以做基於統計模型的進一步假設以改進經驗機率:如果這個模型合適,則它可以被用來推導一個特定事件的機率。
優點
使用經驗機率來估算機率的一大優點既是這種方法相對不需要很多假設條件。
例如,估計一群男性中滿足兩個條件的人的機率:
a. 他們超過六英尺高;
b. 比起覆盆子果醬,他們更喜歡草莓醬。
直接估算方法是可以數出這群男性中同時滿足這兩個條件的人數以得出經驗機率值。另一種估算方法可以首先算出這一男性群體中身高超過六英尺的比例,以及喜歡草莓醬多過覆盆子醬的比率,但這一估算法的前提是假設這兩個條件是彼此獨立的。
缺點
使用經驗機率估進行對機率的估算在機率極低或極高(接近於0或1)時可能會出現問題。在這種情況下,我們需要非常大的樣本量以保證估算的相對準確性。這時,根據具體情況我們可以藉助統計模型進行估算,通常而言,在假設成立的情況下,這樣的模型可以幫助改進經驗機率的準確度。
例如,要估算任意一年的二月份中最低的日最高溫度低於零度的機率。過去幾年的溫度幾可以用來估計這個機率。或者可以選擇一個機率分布模型,用它來擬合過去幾年的觀測值。擬合成功的分布模型可以用來估算我們需要的機率。使用這種方法,即使過去所有幾率這一天的最高溫度都高於零度,我們依然可以進行機率估算。
3. 容易混淆的概念:
在英語中,經驗機率有時也被稱為歸納機率posteriori probability,注意不要和貝葉斯理論中的後驗機率(posterior probability)向混淆。前者第一個單詞後面多加了一個i。

